Video hướng dẫn giải
Cho tổng \(\displaystyle{S_n} = {1 \over {1.2}} + {1 \over {2.3}} + ... + {1 \over {n(n + 1)}}\) với \(n\in {\mathbb N}^*\).
LG a
Tính \({S_1},{S_2},{S_3}\)
Phương pháp giải:
Tính các giá trị \(S_1;S_2;S_3\) bằng cách thay lần lượt \(n=1;n=2;n=3\).
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {S_1} = {1 \over {1.2}} = {1 \over 2} \cr
& {S_2} = {1 \over {1.2}} + {1 \over {2.3}} = {2 \over 3} \cr
& {S_3} = {1 \over {1.2}} + {1 \over {2.3}} + {1 \over {3.4}} = {3 \over 4} \cr} \)
LG b
Dự đoán công thức tính tổng \(S_n\) và chứng minh bằng quy nạp.
Phương pháp giải:
Dựa vào các giá trị \(S_1;S_2;S_3\) tính được ở trên, dự đoán tổng \(S_n\).
Chứng minh kết quả vừa dự đoán bằng phương pháp quy nạp toán học.
Lời giải chi tiết:
Từ câu a) ta dự đoán \(\displaystyle {S_n} = {n \over {n + 1}}(1)\), với mọi \(n\in {\mathbb N}^*\)
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi \(n = 1\), vế trái là \(\displaystyle {S_1} = {1 \over 2}\) vế phải bằng \(\displaystyle {1 \over {1 + 1}} = {1 \over 2}\).
Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với \(n\ge 1\), tức là
\(\displaystyle {S_k} = {1 \over {1.2}} + {1 \over {2.3}} + ... + {1 \over {k(k + 1)}} = {k \over {k + 1}}\)
Ta phải chứng minh đẳng thức đúng với \(n = k + 1\), nghĩa là phải chứng minh: \(\displaystyle {S_{k + 1}} = {{k + 1} \over {k + 2}}\)
Ta có :
\(\displaystyle {S_{k + 1}} = {S_k} + {1 \over {(k + 1)(k + 2)}} \)\(\displaystyle = {k \over {k + 1}} + {1 \over {(k + 1)(k + 2)}}\)
\( = \dfrac{{k\left( {k + 2} \right) + 1}}{{\left( {k + 1} \right)\left( {k + 2} \right)}}\) \(\displaystyle = {{{k^2} + 2k + 1} \over {(k + 1)(k + 2)}} \)
\(= \frac{{{{\left( {k + 1} \right)}^2}}}{{\left( {k + 1} \right)\left( {k + 2} \right)}}\) \(= {{k + 1} \over {k + 2}}\)
tức là đẳng thức (1) đúng với \(n = k + 1\).
Vậy đẳng thức (1) đã được chứng minh.
Chú ý:
Một cách dự đoán khác các em có thể tham khảo thêm như sau:
\(\begin{array}{l}
\;{S_1} = \frac{1}{{1.2}} = \frac{1}{1} - \frac{1}{2} = 1 - \frac{1}{2}\\
{S_2} = \frac{1}{{1.2}} + \frac{1}{{2.3}} = \left( {\frac{1}{1} - \frac{1}{2}} \right) + \left( {\frac{1}{2} - \frac{1}{3}} \right) = 1 - \frac{1}{3}\\
{S_3} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} = \left( {\frac{1}{1} - \frac{1}{2}} \right) + \left( {\frac{1}{2} - \frac{1}{3}} \right) + \left( {\frac{1}{3} - \frac{1}{4}} \right) = 1 - \frac{1}{4}
\end{array}\)
Dự đoán: \({S_n} = 1 - \frac{1}{{n + 1}}\) (1)
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với \(n = 1\) thì (1) đúng.
+ Giả sử (1) đúng với \(n = k\), tức là
\[{S_k} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{k\left( {k + 1} \right)}} = 1 - \frac{1}{{k + 1}}\]
Khi đó,
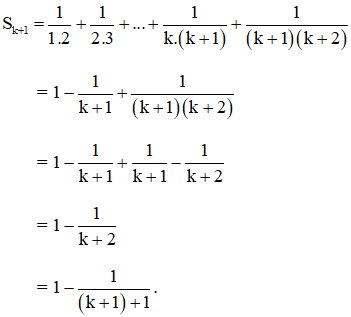
\( \Rightarrow \left( 1 \right){\rm{ }} \text {đúng với } \, n = {\rm{ }}k + 1, \text {do đó đúng }{\rm{ }}\forall {\rm{ }}n{\rm{ }} \in {\rm{ }}N*.\)

