Đề bài
Cho hình chữ nhật \(ABCD, AC\) và \(BD\) cắt nhau tại \(I\). Gọi \(H, K, L\) và \(J\) lần lượt là trung điểm của \(AD, BC, KC\) và \(IC\). Chứng minh hai hình thang \(JLKI\) và \(IHDC\) đồng dạng với nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thực hiện liên tiếp hai phép biến hình sau:
- Phép vị tự tâm \(C\) tỉ số \(2.\)
- Phép đối xứng tâm \(I.\)
Lời giải chi tiết

Ta có: \(J, L, K, I\) là trung điểm của \(CI, CK, CB, CA\) nên
\(\overrightarrow{CI}=2\overrightarrow{CJ}\) \(\Rightarrow {V_{\left( {C,2} \right)}}\left( J \right) = I\)
\(\overrightarrow{CK}=2\overrightarrow{CL}\) \(\Rightarrow {V_{\left( {C,2} \right)}}\left( L \right) = K,\)
\(\overrightarrow{CB}=2\overrightarrow{CK}\) \(\Rightarrow {V_{\left( {C,2} \right)}}\left( K \right) = B,\)
\(\overrightarrow{CA}=2\overrightarrow{CI}\) \({V_{\left( {C,2} \right)}}\left( I \right) = A\)
Do đó \({V_{\left( {C,2} \right)}}\left( {JLKI} \right) = IKBA\).
Lại có, \({D_I}\left( I \right) = I,{D_I}\left( K \right) = H\)
\({D_I}\left( B \right) = D,{D_I}\left( A \right) = C\)
Nên \({D_I}\left( {IKBA} \right) = IHDC\).
Do đó tồn tại phép đồng dạng (hợp bởi phép vị tự và phép đối xứng tâm) biến hình thang \(JLKI\) thành hình thang \(IHDC\).
Vậy hai hình thang \(JLKI\) và hình thang \(IHDC\) đồng dạng.
Cách khác:
+ \(I\) là trung điểm \(AC; BD; HK\)
\( \Rightarrow {\rm{ }}{_I}\left( H \right) = K{\rm{ }};{_I}\left( D \right) = B{\rm{ }};{_I}\;\left( C \right) = {\rm{ }}A.\)
\(⇒\) Hình thang \(IKBA\) đối xứng với hình thang \(IHDC\) qua \(I\) (1)
+ \(J; L; K; I\) lần lượt là trung điểm của \(CI; CK; CB; CA\)
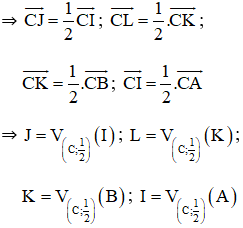
\(⇒\) Hình thang \(JLKI\) là ảnh của hình thang \(IKBA\) qua phép vị tự tâm \(C\) tỉ số \(\frac 1 2\)
\(⇒\) Hình thang \(JLKI\) là ảnh của hình thang \(IHDC\) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm \(I\) và phép vị tự tâm\( C\) tỉ số \(\frac 1 2\).
\(⇒ IJKI\) và \(IHDC\) đồng dạng.

