Đề bài
Chọn hệ tọa độ OxyOxy sao cho trục OxOx trùng với trục đối xứng, rồi dùng biểu thức tọa độ của phép đối xứng qua trục OxOx để chứng minh tính chất 1.
Video hướng dẫn giải
Lời giải chi tiết
Gọi A(xA;yA),B(xB;yB)A(xA;yA),B(xB;yB)
Xét phép đối xứng qua trục OxOx thì A,BA,B biến thành A′(xA;−yA),B′(xB;−yB)
Khi đó:
AB=√(xB−xA)2+(yB−yA)2A′B′=√(xB−xA)2+(−yB+yA)2=√(xB−xA)2+(yB−yA)2=AB⇒A′B′=AB⇒dpcm
Chú ý:
Trực quan các em có thể lấy hai điểm A,B cụ thể như sau:
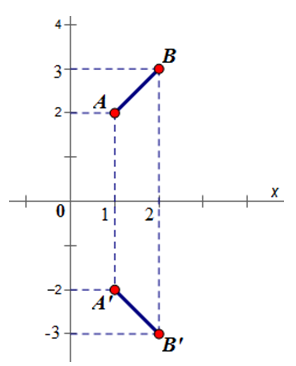
Lấy ảnh A′,B′ của hai điểm A(1;2) và B(2;3) qua phép đối xứng trục Ox
Dùng biểu thức tọa độ của phép đối xứng qua trục Ox, ta có:
A′(1;−2),B′(2;−3)
AB=√(2−1)2+(3−2)2=√12+12=√2A′B′=√(2−1)2+(−3−(−2))2=√12+(−1)2=√2
⇒A′B′=AB