Đề bài
Trong mặt phẳng tọa độ OxyOxy cho điểm A(2;0)A(2;0) và đường thẳng dd có phương trình x+y−2=0x+y−2=0. Tìm ảnh của AA và dd qua phép quay tâm OO góc 90∘90∘.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng hình vẽ trên mặt phẳng tọa độ OxyOxy, quay ngược chiều kim đồng hồ.
Ảnh của đường thẳng được xác định bởi ảnh của ít nhất 2 điểm thuộc đường thẳng ấy
Lời giải chi tiết
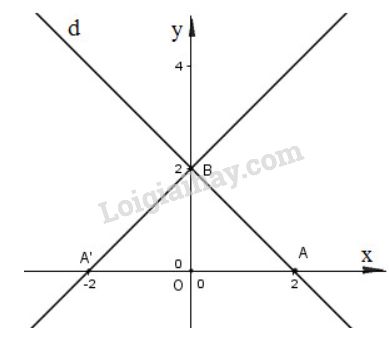
* Ta có A(2;0)A(2;0) thuộc tia Ox.Ox.
Gọi Q(O,90)(A)=BQ(O,90)(A)=B thì BB thuộc tia OyOy và OA=OBOA=OB nên B(0;2).B(0;2).
* Lấy A(2;0),B(0;2)A(2;0),B(0;2) thuộc dd
Ta có: Q(O;900)(A)=B⇒B(0;2)Q(O;900)(A)=B⇒B(0;2)
Q(O;900)(B)=A′⇒A′(−2;0)
Do đó Q(O;900) biến đường thẳng AB thành đường thẳng BA′ hay biến đường thẳng d thành đường thẳng BA′.
Mà B(0;2),A′(−2;0) nên đường thẳng A′B có phương trình x−2+y2=1
⇔−x+y=2 ⇔x−y+2=0
Chú ý: Phương trình đường thẳng theo đoạn chắn A(a;0),B(0;b) ⇒AB:xa+yb=1 với ab≠0.
Cách khác:
Gọi d′ là ảnh của d qua Q(O;900)
Dễ thấy A(2;0) thuộc d vì 2+0−2=0.
Q(O;900)(A)=B⇒B(0;2) thuộc d′.
Do d′=Q(O;900)(d) ⇒(d,d′)=900⇒d′⊥d.
Mà →nd=(1;1)⇒→nd′=(1;−1) là VTPT của d′.
d′ đi qua B(0;2) và nhận (1;−1) làm VTPT nên có phương trình:
1(x−0)−1(y−2)=0 hay x−y+2=0.

