Đề bài
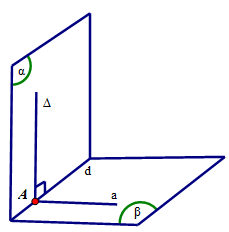
Cho hai mặt phẳng \((α)\) và \((β)\) vuông góc với nhau và cắt nhau theo giao tuyến \(d\). Chứng minh rằng nếu có một đường thẳng \(Δ\) nằm trong \((α)\) và \(Δ\) vuông góc với \(d\) thì \(Δ\) vuông góc với \((β)\)
Video hướng dẫn giải
Lời giải chi tiết
\(Δ\) nằm trong \((α)\) và \(Δ\) vuông góc với \(d ⇒ Δ\) cắt \(d\) tại \(A\)
Từ \(A,\) vẽ đường thẳng \(a\) thuộc \((β)\) và \(a ⊥ d\)
Vì \((α) ⊥ (β)\) nên góc giữa \(Δ\) và \(a\) là \(90^0\) hay \(Δ ⊥ a\)
\(⇒ Δ ⊥ (d,a)\) hay \(Δ ⊥ (β)\)