Đề bài
A. TRẮC NGHIỆM (5,0 điểm)
Câu 1: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu a // b và \(\left( \alpha \right) \bot a\) thì \(\left( \alpha \right) \bot b\).
B. Nếu \(\left( \alpha \right)\parallel \left( \beta \right)\) và \(a \bot \left( \alpha \right)\) thì \(a \bot \left( \beta \right)\).
C. Nếu \(\left( \alpha \right)\) và \(\left( \beta \right)\) là hai mặt phẳng phân biệt và \(a \bot \left( \alpha \right)\), \(a \bot \left( \beta \right)\) thì \(\left( \alpha \right)\parallel \left( \beta \right)\).
D. Nếu \(a\parallel \left( \alpha \right)\) và \(b \bot a\) thì \(b \bot \left( \alpha \right)\).
Câu 2: Tìm đạo hàm của hàm số \(y = 3\cos x + 1\).
A. \(y' = 3\sin x\)
B. \(y' = - 3\sin x + 1\)
C. \(y' = - 3\sin x\)
D. \(y' = - \sin x\)
Câu 3: Tính \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} + 3x - 4}}{{\left| {x - 1} \right|}}\).
A. 5 B. 0
C. \( + \infty \) D. -5
Câu 4: Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x}\,\,\,khi\,\,x \ne 0\\3a - 5b - 1\,\,\,\,khi\,\,x = 0\end{array} \right.\). Tìm điều kiện của tham số a và b để hàm số liên tục tại điểm \(x = 0\).
A. \(2a - 6b = 1\)
B. \(2a - 4b = 1\)
C. \(16a - 33b = 6\)
D. \(a - 8b = 1\)
Câu 5: Cho hàm số \(y = {\sin ^2}x\). Mệnh đề nào dưới đây đúng?
A. \(4y.{\cos ^2}x - {\left( {y'} \right)^2} = - 2{\sin ^2}2x\)
B. \(4y{\cos ^2}x - {\left( {y'} \right)^2} = 0\)
C. \(2\sin x - y' = 0\)
D. \({\sin ^2}x + y' = 1\)
Câu 6: Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\) và đáy ABCD là hình vuông. Mệnh đề nào dưới đây đúng?
A. \(\left( {SAC} \right) \bot \left( {SBD} \right)\)
B. \(\left( {SAD} \right) \bot \left( {SBC} \right)\)
C. \(AC \bot \left( {SAB} \right)\)
D. \(BD \bot \left( {SAD} \right)\)
Câu 7: Tìm vi phân của hàm số \(y = 3{x^2} - 2x + 1\).
A. \(dy = 6x - 2\)
B. \(dy = \left( {6x - 2} \right)dx\)
C. \(dx = \left( {6x - 2} \right)dy\)
D. \(dy = 6x - 2dx\)
Câu 8: Một chất điểm chuyển động theo phương trình \(S = {t^3} + 5{t^2} - 5\), trong đó \(t > 0\), t được tính bằng giây (s) và S được tính bằng mét (m). Tính vận tốc của chất điểm tại thời điểm \(t = 2\) (giây).
A. 32 m/s B. 22 m/s
C. 27 m/s D. 28 m/s
Câu 9: Tính \(\mathop {\lim }\limits_{x \to 4} \frac{{x + 5}}{{x - 1}}\).
A. 3 B. 1
C. -5 D. \( + \infty \)
Câu 10: Cho chóp tứ giác đều S.ABCD có AB = a và \(SB = \frac{{a\sqrt 3 }}{2}\). Tính khoảng cách từ A đến mặt phẳng (SBC).
A. \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{a\sqrt 2 }}{4}\)
B. \(d\left( {A;\left( {SBC} \right)} \right) = \frac{a}{2}\)
C. \(d\left( {A;\left( {SBC} \right)} \right) = a\)
D. \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{a\sqrt 2 }}{2}\)
Câu 11: Cho tứ diện ABCD, gọi G là trọng tâm của tam giác BCD. Mệnh đề nào dưới đây đúng?
A. \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \)
D. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
Câu 12: Tính \(\lim \frac{{5n + 1}}{{3n + 7}}\).
A. \(\frac{5}{7}\) B. \(\frac{5}{3}\)
C. \(\frac{1}{7}\) D. \(0\)
Câu 13: Tìm đạo hàm cấp hai của hàm số \(y = \frac{1}{{x + 2}}\).
A. \(y'' = \frac{2}{{{{\left( {x + 2} \right)}^3}}}\)
B. \(y'' = \frac{{ - 2}}{{{{\left( {x + 2} \right)}^3}}}\)
C. \(y'' = \frac{{ - 1}}{{{{\left( {x + 2} \right)}^3}}}\)
D. \(y'' = \frac{1}{{{{\left( {x + 2} \right)}^3}}}\)
Câu 14: Cho hình lập phương ABCD.A’B’C’D’. Gọi \(\alpha \) là góc giữa hai đường thẳng A’B và CB’. Tính \(\alpha \).
A. \(\alpha = {30^0}\) B. \(\alpha = {45^0}\)
C. \(\alpha = {60^0}\) D. \(\alpha = {90^0}\)
Câu 15: Tìm đạo hàm của hàm số \(y = {x^3} - 2x\).
A. \(y' = 3x - 2\)
B. \(y' = 3{x^2} - 2\)
C. \(y' = {x^3} - 2\)
D. \(y' = 3{x^2} - 2x\)
B. PHẦN TỰ LUẬN (5,0 điểm)
Bài 1 (2,0 điểm):
a) Tìm \(\lim \frac{{5 + n}}{{4 - n}}\).
b) Tìm \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{x - 3}}\).
c) Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 7x + 10}}{{x - 5}}\,\,\,khi\,\,x \ne 5\\\,\,\,\,\,2m - 1\,\,\,\,\,\,\,\,\,\,khi\,\,x = 5\end{array} \right.\). Tìm điều kiện của tham số m để hàm số liên tục tại \(x = 5\)
Bài 2 (1,0 điểm): Cho hàm số \(y = f\left( x \right) = {x^3} + {x^2} - 1\) có đồ thị \(\left( C \right)\).
a) Tính đạo hàm của hàm số trên.
b) Viết phương trình tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm có hoành độ \({x_0} = 1\).
Bài 3 (2,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a; các cạnh bên của hình chóp cùng bằng \(a\sqrt 3 \).
a) Chứng minh rằng \(BD \bot \left( {SAC} \right)\).
b) Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (P).
c) Tính góc giữa đường thẳng AB và mặt phẳng (P).
Lời giải chi tiết
A. TRẮC NGHIỆM (5,0 điểm)
| 1. D | 2. C | 3. D | 4. C | 5. B |
| 6. A | 7. B | 8. A | 9. A | 10. D |
| 11. D | 12. B | 13. A | 14. C | 15. B |
Câu 1 (TH):
Phương pháp:
Sử dụng các quan hệ song song, vuông góc trong không gian.
Cách giải:
Dễ thấy đáp án D sai, minh họa như hình vẽ dưới đây cho thấy \(b\parallel \left( \alpha \right)\).
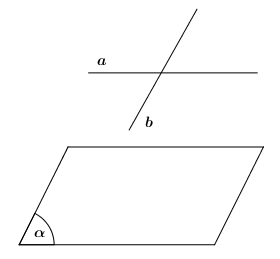
Chọn D.
Câu 2 (NB):
Phương pháp:
Sử dụng công thức đạo hàm hàm số lượng giác: \(\left( {\cos x} \right)' = - \sin x\).
Cách giải:
Ta có: \(y' = - 3\sin x\).
Chọn C.
Câu 3 (TH):
Phương pháp:
- Xét dấu để phá trị tuyệt đối.
- Phân tích tử thành nhân tử và rút gọn sau đó tính giới hạn.
Cách giải:
Khi \(x \to {1^ - }\) thì \(x < 1 \Rightarrow x - 1 < 0\) nên \(\left| {x - 1} \right| = - \left( {x - 1} \right)\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} + 3x - 4}}{{\left| {x - 1} \right|}}\\ = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left( {x - 1} \right)\left( {x + 4} \right)}}{{ - \left( {x - 1} \right)}}\\ = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x - 4} \right) = - 1 - 4 = - 5.\end{array}\)
Chọn D.
Câu 4 (VD):
Phương pháp:
- Để hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
- Để tính \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\), ta thêm bớt và tách thành 2 giới hạn dạng 0/0, sau đó sử dụng phương pháp nhân liên hợp.
Cách giải:
TXĐ: \(D = \mathbb{R},\,\,x = 0 \in D\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - 1}}{x} + \mathop {\lim }\limits_{x \to 0} \frac{{1 - \sqrt {1 - bx} }}{x}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {\sqrt[3]{{ax + 1}} - 1} \right)\left( {{{\sqrt[3]{{ax + 1}}}^2} + \sqrt[3]{{ax + 1}} + 1} \right)}}{{x\left( {{{\sqrt[3]{{ax + 1}}}^2} + \sqrt[3]{{ax + 1}} + 1} \right)}}\\ + \mathop {\lim }\limits_{x \to 0} \frac{{\left( {1 - \sqrt {1 - bx} } \right)\left( {1 + \sqrt {1 - bx} } \right)}}{{x\left( {1 + \sqrt {1 - bx} } \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{ax + 1 - 1}}{{x\left( {{{\sqrt[3]{{ax + 1}}}^2} + \sqrt[3]{{ax + 1}} + 1} \right)}}\\ + \mathop {\lim }\limits_{x \to 0} \frac{{1 - 1 + bx}}{{x\left( {1 + \sqrt {1 - bx} } \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{a}{{{{\sqrt[3]{{ax + 1}}}^2} + \sqrt[3]{{ax + 1}} + 1}}\\ + \mathop {\lim }\limits_{x \to 0} \frac{b}{{1 + \sqrt {1 - bx} }}\\ = \frac{a}{{1 + 1 + 1}} + \frac{b}{{1 + 1}}\\ = \frac{a}{3} + \frac{b}{2}\end{array}\)
\(f\left( 0 \right) = 3a - 5b - 1\).
Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\)
\( \Leftrightarrow \frac{a}{3} + \frac{b}{2} = 3a - 5b - 1\) \( \Leftrightarrow \frac{8}{3}a - \frac{{11}}{2}b = 1\)\( \Leftrightarrow 16a - 33b = 6\)
Chọn C.
Câu 5 (VD):
Phương pháp:
- Sử dụng công thức tính đạo hàm hàm hợp và hàm số lượng giác để tính \(y'\).
- Thay \(y'\) vào các đẳng thức ở các đáp án.
Cách giải:
Ta có:
\(\begin{array}{l}y' = \left( {{{\sin }^2}x} \right)' = 2\sin x.\left( {\sin x} \right)'\\\,\,\,\,\, = 2\sin x.\cos x = \sin 2x\end{array}\)
Thay vào đáp án B ta có:
\(\begin{array}{l}\,\,\,\,\,4y{\cos ^2}x - {\left( {y'} \right)^2} = 0\\ \Leftrightarrow 4{\sin ^2}x{\cos ^2}x - {\left( {\sin 2x} \right)^2} = 0\\ \Leftrightarrow {\left( {2\sin x\cos x} \right)^2} - {\left( {\sin 2x} \right)^2} = 0\end{array}\)
\( \Leftrightarrow {\left( {\sin 2x} \right)^2} - {\left( {\sin 2x} \right)^2} = 0\) (luôn đúng).
Chọn B.
Câu 6 (TH):
Phương pháp:
Sử dụng các định lí sau:
+) \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).
+) \(\left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\).
Cách giải:
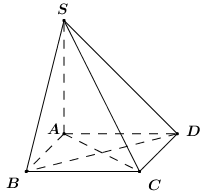
Vì ABCD là hình vuông nên \(AC \bot BD\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
\(\left\{ \begin{array}{l}BD \bot \left( {SAC} \right)\\BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\).
Vậy mệnh đề đúng là A.
Chọn A.
Câu 7 (NB):
Phương pháp:
- Sử dụng công thức tính vi phân: \(y = f\left( x \right) \Rightarrow dy = f'\left( x \right)dx\).
- Sử dụng công thức tính đạo hàm: \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\).
Cách giải:
Ta có:
\(\begin{array}{l}dy = \left( {3{x^2} - 2x + 1} \right)dx\\dy = \left( {6x - 2} \right)dx\end{array}\)
Chọn B.
Câu 8 (NB):
Phương pháp:
Vận tốc của chất điểm tại thời điểm \(t = {t_0}\) được tính theo công thức \(v\left( {{t_0}} \right) = S'\left( {{t_0}} \right)\).
Cách giải:
Ta có:
\(\begin{array}{l}v = s'\left( t \right) = 3{t^2} + 10t\\ \Rightarrow v\left( 2 \right) = {3.2^2} + 10.2 = 32\,\,\left( {m/s} \right)\end{array}\)
Chọn A.
Câu 9 (NB):
Phương pháp:
Hàm số xác định tại \(x = {x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Cách giải:
Ta có: \(\mathop {\lim }\limits_{x \to 4} \frac{{x + 5}}{{x - 1}} = \frac{{4 + 5}}{{4 - 1}} = \frac{9}{3} = 3.\)
Chọn A.
Câu 10 (VD):
Phương pháp:
- Đổi điểm về tính khoảng cách từ O đến (SBC).
- Xác định mặt phẳng chứa O và vuông góc với (SBC).
- Trong mặt phẳng đó kẻ đường thẳng vuông góc với giao tuyến của mặt phẳng đó và (SBC).
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông.
Cách giải:
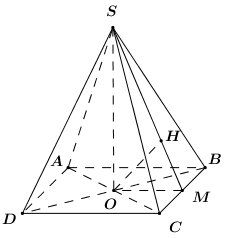
Gọi \(O = AC \cap BD\). Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\).
Ta có: \(AO \cap \left( {SBC} \right) = C\)\( \Rightarrow \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {O;\left( {SBC} \right)} \right)}} = \frac{{AC}}{{OC}} = 2\)
\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right)\).
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\) và \(OM = \frac{1}{2}BC = \frac{1}{2}AB = \frac{a}{2}\). Mà \(AB \bot BC\) nên \(OM \bot BC\).
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right)\).
\(\left\{ \begin{array}{l}BC \bot \left( {SOM} \right)\\BC \subset \left( {SBC} \right)\end{array} \right.\)\( \Rightarrow \left( {SOM} \right) \bot \left( {SBC} \right)\) và \(\left( {SOM} \right) \cap \left( {SBC} \right) = SM\).
Trong (SOM) kẻ \(OH \bot SM\) ta có:
\(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {SOM} \right)\\\left( {SBC} \right) \cap \left( {SOM} \right) = SM\\OH \subset \left( {SOM} \right),\,\,OH \bot SM\end{array} \right.\)\( \Rightarrow OH \bot \left( {SBC} \right)\)
Do đó \(d\left( {O;\left( {SBC} \right)} \right) = OH\) và \(d\left( {A;\left( {SBC} \right)} \right) = 2OH\).
Vì ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \) \( \Rightarrow OB = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOB có: \(SO = \sqrt {S{B^2} - O{B^2}} \)\( = \sqrt {\frac{{3{a^2}}}{4} - \frac{{2{a^2}}}{4}} = \frac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SOM có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}}\)\( = \frac{4}{{{a^2}}} + \frac{4}{{{a^2}}} = \frac{8}{{{a^2}}}\) \( \Rightarrow OH = \frac{{a\sqrt 2 }}{4}\).
Vậy \(d\left( {A;\left( {SBC} \right)} \right) = 2OH = \frac{{a\sqrt 2 }}{2}\).
Chọn D.
Câu 11 (NB):
Phương pháp:
Sử dụng công thức trọng tâm: G là trọng tâm của tam giác BCD thì \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Cách giải:
Vì G là trọng tâm của tam giác BCD thì \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Chọn D.
Câu 12 (NB):
Phương pháp:
Chia cả tử và mẫu cho n.
Cách giải:
\(\lim \frac{{5n + 1}}{{3n + 7}} = \lim \frac{{5 + \frac{1}{n}}}{{3 + \frac{7}{n}}} = \frac{5}{3}.\)
Chọn B.
Câu 13 (TH):
Phương pháp:
Sử dụng công thức tính đạo hàm: \(\left( {\frac{1}{u}} \right)' = \frac{{ - u'}}{{{u^2}}}\).
Cách giải:
Ta có:
\(\begin{array}{l}y' = \left( {\frac{1}{{x + 2}}} \right)' = \frac{{ - \left( {x + 2} \right)'}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - 1}}{{{{\left( {x + 2} \right)}^2}}}\\y'' = \left( {\frac{{ - 1}}{{{{\left( {x + 2} \right)}^2}}}} \right)' = \frac{{\left[ {{{\left( {x + 2} \right)}^2}} \right]'}}{{{{\left( {x + 2} \right)}^4}}}\\ = \frac{{2\left( {x + 2} \right).\left( {x + 2} \right)'}}{{{{\left( {x + 2} \right)}^4}}} = \frac{2}{{{{\left( {x + 2} \right)}^3}}}\end{array}\)
Chọn A.
Câu 14 (VD):
Phương pháp:
- Sử dụng định lí: \(a\parallel b \Rightarrow \angle \left( {a;c} \right) = \angle \left( {b;c} \right)\).
- Áp dụng định lí Cosin trong tam giác: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).
Cách giải:
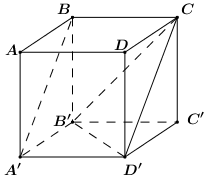
Vì A’BCD’ là hình bình hành (BC = A’D’ và BC // A’D’) nên A’B // CD’
\( \Rightarrow \angle \left( {A'B;CB'} \right) = \angle \left( {CD';CB'} \right)\).
Do BCC’B’, CDD’C’, A’B’C’D’ là các hình vuông cạnh a nên \(B'C = CD' = B'D' = a\sqrt 2 \).
Do đó tam giác B’CD’ là tam giác đều nên \(\angle B'CD' = {60^0}\).
Vậy \(\angle \left( {A'B;CB'} \right) = \angle \left( {CD';CB'} \right)\)\( = \angle B'CD' = {60^0}\) hay \(\alpha = {60^0}\).
Chọn C.
Câu 15 (NB):
Phương pháp:
Sử dụng công thức tính đạo hàm \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\).
Cách giải:
Ta có: \(y' = \left( {{x^3} - 2x} \right)' = 3{x^2} - 2\).
Chọn B.
B. PHẦN TỰ LUẬN (5,0 điểm)
Bài 1:
Phương pháp:
a) Chia cả tử và mẫu cho n.
b) Nhân cả tử và mẫu với biểu thức liên hợp của tử.
Rút gọn để khử dạng 0/0 và tính giới hạn.
c) Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Cách giải:
a) \(\lim \frac{{5 + n}}{{4 - n}} = \lim \frac{{\frac{5}{n} + 1}}{{\frac{4}{n} - 1}} = \frac{1}{{ - 1}} = - 1.\)
b) \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{x + 1 - 4}}{{\left( {x - 3} \right)\left( {\sqrt {x + 1} + 2} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 3} \frac{1}{{\sqrt {x + 1} + 2}} = \frac{1}{{\sqrt 4 + 2}} = \frac{1}{4}.\)
c) TXĐ: \(D = \mathbb{R},\,\,x = 5 \in D\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 5} f\left( x \right) = \mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 7x + 10}}{{x - 5}}\\ = \mathop {\lim }\limits_{x \to 5} \frac{{\left( {x - 5} \right)\left( {x - 2} \right)}}{{x - 5}}\\ = \mathop {\lim }\limits_{x \to 5} \left( {x - 2} \right) = 5 - 2 = 3.\\f\left( 5 \right) = 2m - 1\end{array}\)
Để hàm số liên tục tại \(x = 5\) thì \(\mathop {\lim }\limits_{x \to 5} f\left( x \right) = f\left( 5 \right)\) \( \Leftrightarrow 2m - 1 = 3 \Leftrightarrow m = 2.\)
Bài 2:
Phương pháp:
a) Sử dụng công thức tính đạo hàm \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\).
b) Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
Cách giải:
a) \(f'\left( x \right) = 3{x^2} + 2x\).
b) Ta có: \(f'\left( 1 \right) = {3.1^2} + 2.1 = 5\) và \(f\left( 1 \right) = {1^3} + {1^2} - 1 = 1\).
Vậy phương trình tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm có hoành độ \({x_0} = 1\) là:
\(y = 5\left( {x - 1} \right) + 1 = 5x - 4\).
Bài 3:
Cách giải:
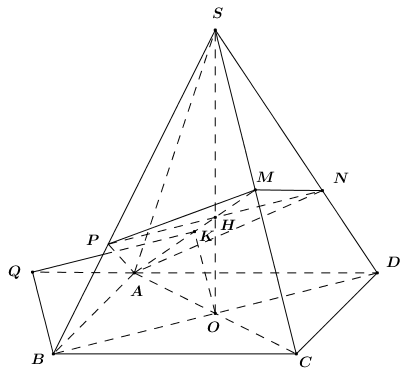
Gọi \(O = AC \cap BD\). Vì chóp S.ABCD có tất cả các cạnh bên bằng nhau nên \(SO \bot \left( {ABCD} \right)\).
a) Vì ABCD là hình vuông nên \(AC \bot BD\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow BD \bot \left( {SAC} \right)\)
b) Trong (SAC) kẻ \(AM \bot SC\,\,\left( {M \in SC} \right)\) \( \Rightarrow AM \subset \left( P \right)\).
Trong (SAC) gọi \(AM \cap SO = H\).
Ta có: \(BD \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BD \bot SC\).
Mà \(\left( P \right) \bot SC \Rightarrow BD\parallel \left( P \right)\).
Xét (P) và (SBD) có:
H là điểm chung
\(BD \subset \left( {SBD} \right),\,\,BD\parallel \left( P \right)\)
\( \Rightarrow \) Giao tuyến (P) và (SBD) là đường thẳng đi qua H và song song với BD.
Trong (SBD) qua H kẻ NP // BD \(\left( {N \in SD,\,\,P \in SA} \right)\).
Khi đó thiết diện của hình chóp cắt bởi (P) là tứ giác ANMP.
c) Trong (SAC) kẻ \(OK \bot AM\,\,\left( {K \in AM} \right)\).
Ta có: \(BD \bot \left( {SAC} \right)\,\,\,\left( {cmt} \right),\,\,\)\(BD\parallel \left( P \right)\) \( \Rightarrow \left( P \right) \bot \left( {SAC} \right)\).
\(\left\{ \begin{array}{l}\left( P \right) \bot \left( {SAC} \right)\\\left( P \right) \cap \left( {SAC} \right) = AM\\OK \subset \left( {SAC} \right),\,\,OK \bot AM\end{array} \right.\)\( \Rightarrow OK \bot \left( P \right)\)
Hạ \(BQ \bot \left( P \right)\) ta có: \(OB\parallel PN\,\,\,\left( {do\,\,BD\parallel PN} \right)\)
\( \Rightarrow d\left( {B;\left( P \right)} \right) = d\left( {O;\left( P \right)} \right)\)\( \Rightarrow BQ = OK\)
\( \Rightarrow \) AQ là hình chiếu của AB lên (P) \( \Rightarrow \angle \left( {AB;\left( P \right)} \right) = \angle \left( {AB;AQ} \right)\).
Ta có: \(\left\{ \begin{array}{l}OK \bot \left( P \right)\\SC \bot \left( P \right)\,\,\left( {gt} \right)\end{array} \right.\)\( \Rightarrow OK\parallel SC \Rightarrow OK\parallel CM\)
Lại có O là trung điểm của AC nên suy ra K là trung điểm của AM (định lí đường trung bình của tam giác).
\( \Rightarrow OK\) là đường trung bình của tam giác AMC \( \Rightarrow OK = \frac{1}{2}MC\).
Vì ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \).
Xét tam giác SAC ta có:
\(\begin{array}{l}\cos \angle SCA\\ = \frac{{A{C^2} + S{C^2} - S{A^2}}}{{2AC.SC}}\\ = \frac{{2{a^2} + 3{a^2} - 3{a^2}}}{{2.a\sqrt 2 .a\sqrt 3 }} = \frac{{\sqrt 6 }}{6}\end{array}\)
Xét tam giác vuông AMC có: \(MC = AC.\cos \angle SCA\)\( = a\sqrt 2 .\frac{{\sqrt 6 }}{6} = \frac{{a\sqrt 3 }}{3}\)
\( \Rightarrow OK = \frac{1}{2}MC = \frac{{a\sqrt 3 }}{6} = PQ\).
Ta có \(BQ \bot \left( P \right) \Rightarrow BQ \bot AQ\) \( \Rightarrow \Delta ABQ\) vuông tại Q.
\( \Rightarrow \sin \angle BAQ = \frac{{BQ}}{{AB}} = \frac{{\sqrt 3 }}{6}\).
Vậy \(\angle BAQ \approx {16^0}47'\).
Nguồn: Sưu tầm
