Đề bài
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a,BC=b,CC′=c.
a) Chứng minh rằng mặt phẳng (ADC′B′) vuông góc với mặt phẳng (ABB′A′).
b) Tính độ dài đường chéo AC′ theo a,b,c.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh DA⊥(ABB′A′)
b) Sử dụng định lí Pytago.
Lời giải chi tiết
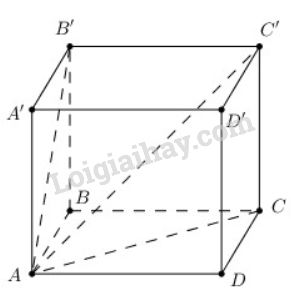
a) Ta có:
{DA⊥AA′DA⊥AB⇒DA⊥(ABB′A′)
Mà DA⊂(ADC′B′)
⇒(ADC′B′)⊥(ABB′A′).
b)
{C′C⊥CDC′C⊥CB⇒C′C⊥(ABCD)
Mà CA⊂(ABCD)⇒C′C⊥CA hay tam giác ACC′ vuông tại C.
Xét tam giác vuông ACC′
AC′=√AC2+CC′2 =√AD2+DC2+CC′2
=√a2+b2+c2.
Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.

