1. Bài toán tính khoảng cách từ một điểm đến một đường thẳng
Phương pháp:
Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác định được hình chiếu H của điểm M trên đường thẳng Δ, rồi xem MH là đường cao của một tam giác nào đó để tính.
Điểm H thường được dựng theo hai cách sau:
Cách 1: Trong mp(M,Δ) vẽ MH⊥Δ⇒d(M,Δ)=MH
Cách 2: Dựng mặt phẳng (α) qua M và vuông góc với Δ tại H.
Khi đó d(M,Δ)=MH.
Hai công thức sau thường được dùng để tính MH
CT1: ΔMAB vuông tại M và có đường cao MH thì 1MH2=1MA2+1MB2.
CT2: MH là đường cao của ΔMAB thì MH=2SMABAB.
2. Tính khoảng cách từ một điểm đến một mặt phẳng
Phương pháp:
Để tính được khoảng từ điểm Mđến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm M trên (α).
TH1:
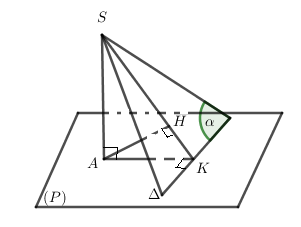
- Dựng AK⊥Δ⇒Δ⊥(SAK)⇒(α)⊥(SAK) và (α)∩(SAK)=SK.
- Dựng AH⊥SK⇒AH⊥(α)⇒d(A,(α))=AH
TH2:
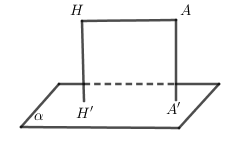
- Tìm điểm H∈(α) sao cho AH//(α)⇒d(A,(α))=d(H,(α))
TH3:
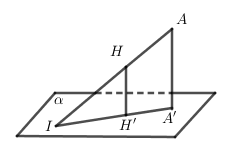
- Tìm điểm H sao cho AH∩(α)=I
- Khi đó: d(A,(α))d(H,(α))=IAIH⇒d(A,(α))=IAIH.d(H,(α))
Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với tứ diện vuông (tương tư như hệ thức lượng trong tam giác vuông) là:
Nếu tứ diện OABC có OA,OB,OC đôi một vuông góc và có đường cao OH thì 1OH2=1OA2+1OB2+1OC2.
3. Phương pháp tính khoảng cách giữa hai đường thẳng
Phương pháp:
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:
+) Phương pháp 1: Dựng đoạn vuông góc chung MN của a và b, khi đó d(a,b)=MN.
Một số trường hợp hay gặp khi dựng đoạn vuông góc chung của hai đường thẳng chéo nhau:
Trường hợp 1: Δ và Δ′ vừa chéo nhau vừa vuông góc với nhau
- Bước 1: Chọn mặt phẳng (α) chứa Δ′ và vuông góc với Δ tại I.
- Bước 2: Trong mặt phẳng (α) kẻ IJ⊥Δ′.
Khi đó IJ là đoạn vuông góc chung và d(Δ,Δ′)=IJ.
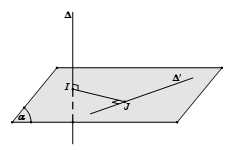
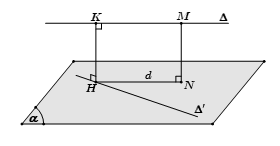
Trường hợp 2: Δ và Δ′ chéo nhau mà không vuông góc với nhau
- Bước 1: Chọn mặt phẳng (α) chứa Δ′ và song song với Δ.
- Bước 2: Dựng d là hình chiếu vuông góc của Δ xuống (α) bằng cách lấy điểm M∈Δ dựng đoạn MN⊥(α), lúc đó d là đường thẳng đi qua N và song song với Δ.
- Bước 3: Gọi H=d∩Δ′, dựng HK//MN
Khi đó HK là đoạn vuông góc chung và d(Δ,Δ′)=HK=MN.
Hoặc
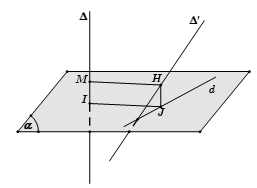
- Bước 1: Chọn mặt phẳng (α)⊥Δ tại I.
- Bước 2: Tìm hình chiếu d của Δ′ xuống mặt phẳng (α).
- Bước 3: Trong mặt phẳng (α), dựng IJ⊥d, từ J dựng đường thẳng song song với Δ cắt Δ′ tại H, từ H dựng HM//IJ.
Khi đó HM là đoạn vuông góc chung và d(Δ,Δ′)=HM=IJ.
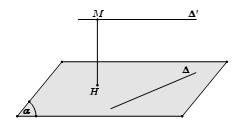
+) Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng Δ và song song với Δ′. Khi đó d(Δ,Δ′)=d(Δ′,(α))
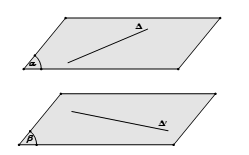
+) Phương pháp 3: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
+) Phương pháp 4: Sử dụng phương pháp vec tơ
a) MN là đoạn vuông góc chung của AB và CD khi và chỉ khi {→AM=x→AB→CN=y→CD→MN.→AB=0→MN.→CD=0
b) Nếu trong (α) có hai vec tơ không cùng phương →u1,→u2 thì OH=d(O,(α))⇔{→OH⊥→u1→OH⊥→u2H∈(α)⇔{→OH.→u1=0→OH.→u2=0H∈(α)

