Đề bài
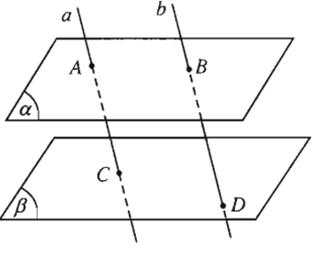
Cho hai mặt phẳng \((α)\) và \((β)\) song song với nhau. Đường thẳng \(a\) cắt \((α)\) và \((β)\) lần lượt tại \(A\) và \(C\). Đường thẳng \(b\) song song với \(a\) cắt \((α)\) và \((β)\) lần lượt tại \(B\) và \(D\).
Hình 2.72 minh họa nội dung trên đúng hay sai?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lí 3 trang 67: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song.
Lời giải chi tiết
Sai vì theo đề bài ta có: \((α) // (β)\)
\(a//b\) nên \(A,B,C,D\) thuộc cùng một mặt phẳng \((ABCD).\)
\(AB\) là giao tuyến của \((α)\) và \((ABDC)\)
\(CD\) là giao tuyến của \((β)\) và \((ABDC)\)
\(⇒ AB // CD\) (theo định lí 3 trang 67)
Hình 2.72 không biểu diễn được \(AB // CD.\)