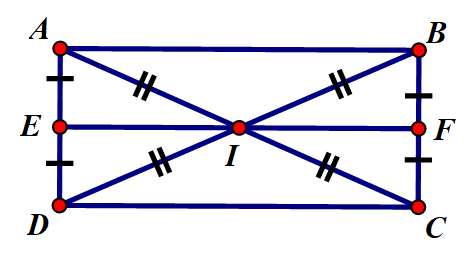
Đề bài
Cho hình chữ nhật ABCD. Gọi I là giao điểm của AC và BD. Gọi E,F theo thứ tự là trung điểm của AD và BC. Chứng minh rằng các hình thang AEIB và CFID bằng nhau.
Video hướng dẫn giải
Lời giải chi tiết
I là giao điểm AC và BD nên I là trung điểm của AC và BD
Mà AC=BD⇒AI=BI=12AC=12BD
Gọi E,F theo thứ tự là trung điểm của AD và BC⇒EF là đường trung bình của hình chữ nhật ABCD và AE=BF=12AD=12BC
⇒EF//AB⇒EF vuông góc với AD và EF vuông góc với BC
Xét hai tam giác vuông AEI và BFI có:
AI=BI
AE=BF
⇒ΔAEI=ΔBFI (cạnh huyền – cạnh góc vuông)
⇒EI=FI (hai cạnh tương ứng)
⇒I là trung điểm EF
Do đó, phép đối xứng qua tâm I biến hình thang AEIB thành hình thang CFID
⇒ Hai hình thang AEIB và CFID bằng nhau.