Đề bài
Bài 1: (1,5 điểm) Tìm các giới hạn sau:
1) lim
2) \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 2x - {x^3}}}{{{x^3} - 3{x^2} + 5}}
3) \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x + 3}}{{x - 3}}
Bài 2: (1,0 điểm) Tìm m để hàm số f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} - 5} - \sqrt {2x - 2} }}{{2{x^2} - 6x}}\,\,khi\,\,x \ne 3\\2m - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 3\end{array} \right. liên tục tại {x_0} = 3.
Bài 3: (1,0 điểm) Tính đạo hàm của các hàm số sau:
1) y = \frac{{\sin x}}{x}
2) y = \left( {x - 2} \right)\left( {{x^5} + 3x - 1} \right)
Bài 4: (1,0 điểm) Cho hàm số y = x + \sqrt {{x^2} + 1} . Chứng minh y = \left( {{x^2} + 1} \right)y'' + xy'.
Bài 5: (1,5 điểm) Cho hàm số y = \frac{{x + 1}}{{x - 2}} có đồ thị \left( C \right). Viết phương trình tiếp tuyến với \left( C \right), biết tiếp tuyến song song với đường thẳng d:\,3x + y - 4 = 0.
Bài 6: (4,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết AD = 4a,\,\,AB = BC = 2a, SA \bot \left( {ABCD} \right) và SC = a\sqrt {10} . Gọi E là trung điểm của AD.
1) Chứng minh BC \bot \left( {SAB} \right).
2) Xác định góc giữa SC và mp\left( {ABCD} \right).
3) Chứng minh \left( {SBE} \right) \bot \left( {SAC} \right).
4) Tính khoảng cách từ E đến mp\left( {SCD} \right).
Lời giải chi tiết
Bài 1 (TH):
Phương pháp:
1) Phân tích, rút gọn, khử dạng \frac{0}{0}.
2) Chia cả tử và mẫu cho {x^3}.
3) Xét dấu và kết luận.
Cách giải:
1) \mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 3x - 2}}{{{x^2} - 4}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right){{\left( {x + 1} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{{{\left( {x + 1} \right)}^2}}}{{x + 2}} = \frac{9}{4}
2) \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 2x - {x^3}}}{{{x^3} - 3{x^2} + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^3}}} + \frac{2}{{{x^2}}} - 1}}{{1 - \frac{3}{x} + \frac{5}{{{x^3}}}}} = - 1 .
3) \left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {3^ - }} \left( {2x + 3} \right) = 9\\\mathop {\lim }\limits_{x \to {3^ - }} \left( {x - 3} \right) = 0\\x - 3 < 0\,\,\forall x < 3\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x + 3}}{{x - 3}} = - \infty .
Bài 2 (VD):
Phương pháp:
Hàm số y = f\left( x \right) liên tục tại x = {x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right) .
Cách giải:
Ta có:
\begin{array}{l}\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {{x^2} - 5} - \sqrt {2x - 2} }}{{2{x^2} - 6x}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {\sqrt {{x^2} - 5} - \sqrt {2x - 2} } \right)\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}}{{2x\left( {x - 3} \right)\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 5 - 2x + 2}}{{2x\left( {x - 3} \right)\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 2x - 3}}{{2x\left( {x - 3} \right)\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {x + 1} \right)\left( {x - 3} \right)}}{{2x\left( {x - 3} \right)\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{x + 1}}{{2x\left( {\sqrt {{x^2} - 5} + \sqrt {2x - 2} } \right)}} = \frac{4}{{24}} = \frac{1}{6}\\f\left( 3 \right) = 2m - 1\end{array}
Để hàm số liên tục tại {x_0} = 3
\Leftrightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)
\Leftrightarrow 2m - 1 = \frac{1}{6} \Leftrightarrow m = \frac{7}{{12}}
Vậy m = \frac{7}{{12}}.
Bài 3 (TH):
Phương pháp:
Sử dụng các quy tắc tính đạo hàm
\begin{array}{l}\left( {uv} \right)' = u'v + uv'\\\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\end{array}
và các công thức tính đạo hàm cơ bản.
Cách giải:
1) y' = \frac{{\left( {\sin x} \right)'.x - \sin x.x'}}{{{x^2}}} = \frac{{x\cos x - \sin x}}{{{x^2}}} .
2) y' = {x^5} + 3x - 1 + \left( {x - 2} \right)\left( {5{x^4} + 3} \right)
\begin{array}{l}y' = {x^5} + 3x - 1 + 5{x^5} + 3x - 10{x^4} - 6\\y' = 6{x^5} - 10{x^4} + 6x - 7\end{array}
Bài 4 (VD):
Phương pháp:
Sử dụng công thức \left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }} và quy tắc tính đạo hàm: \left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}.
Cách giải:
Ta có:
\begin{array}{l}y' = 1 + \frac{{2x}}{{2\sqrt {{x^2} + 1} }}\\ = 1 + \frac{x}{{\sqrt {{x^2} + 1} }}\\y'' = \frac{{\sqrt {{x^2} + 1} - x\frac{x}{{\sqrt {{x^2} + 1} }}}}{{{x^2} + 1}}\\ = \frac{{{x^2} + 1 - {x^2}}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} }}\\ = \frac{1}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} }}\end{array}
Từ đó ta có:
\begin{array}{l}\left( {{x^2} + 1} \right)y'' + xy'\\ = \left( {{x^2} + 1} \right)\frac{1}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} }}\\ + x\left( {1 + \frac{x}{{\sqrt {{x^2} + 1} }}} \right)\\ = \frac{1}{{\sqrt {{x^2} + 1} }} + x + \frac{{{x^2}}}{{\sqrt {{x^2} + 1} }}\\ = x + \frac{{{x^2} + 1}}{{\sqrt {{x^2} + 1} }}\\ = x + \sqrt {{x^2} + 1} = y\,\,\left( {dpcm} \right)\end{array}
Bài 5 (VD):
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f\left( x \right) tại điểm có hoành độ x = {x_0} là
y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right).
Cách giải:
TXĐ: D = \mathbb{R}\backslash \left\{ 2 \right\}. Ta có y' = \frac{{1.\left( { - 2} \right) - 1.1}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}}.
Gọi M\left( {{x_0};{y_0}} \right) là tiếp điểm của \left( C \right), hệ số góc của tiếp tuyến tại C là k = y'\left( {{x_0}} \right) = \frac{{ - 3}}{{{{\left( {{x_0} - 2} \right)}^2}}}.
Do tiếp tuyến song song với đường thẳng d:\,3x + y - 4 = 0 \Leftrightarrow y = - 3x + 4 nên ta có:
\begin{array}{l}\frac{{ - 3}}{{{{\left( {{x_0} - 2} \right)}^2}}} = - 3\\ \Leftrightarrow {\left( {{x_0} - 2} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} - 2 = 1\\{x_0} - 2 = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3 \Rightarrow M\left( {3;4} \right)\\{x_0} = 1 \Rightarrow M\left( {1; - 2} \right)\end{array} \right.\end{array}
Phương trình tiếp tuyến tại M\left( {3;4} \right) là : y = - 3\left( {x - 3} \right) + 4 \Leftrightarrow y = - 3x + 13 .
Phương trình tiếp tuyến tại M\left( {1; - 2} \right) là : y = - 3\left( {x - 1} \right) - 2 \Leftrightarrow y = - 3x + 1 .
Bài 6 (VD):
Phương pháp:
1) \left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right).
2) Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
3) \left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right).
4) Sử dụng phương pháp đổi đỉnh, chứng minh d\left( {E;\left( {SCD} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SCD} \right)} \right).
Cách giải:
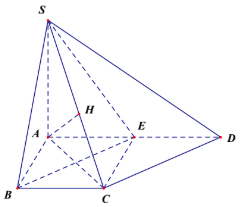
1) Ta có: \left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) .
2) Vì SA \bot \left( {ABCD} \right) \Rightarrow AC là hình chiếu của SC trên \left( {ABCD} \right).
\Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA .
Trong tam giác vuông ABC có:
AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {4{a^2} + 4{a^2}} = 2\sqrt 2 a .
Trong tam giác vuông SAC có:
\cos \angle SCA = \frac{{AC}}{{SC}} = \frac{{2\sqrt 2 a}}{{a\sqrt {10} }} = \frac{{2\sqrt 5 }}{5} \Rightarrow \angle SCA \approx {26^0}34'.
3) Xét tứ giác ABCE có \left\{ \begin{array}{l}AE//BC\\AE = BC = 2a\end{array} \right.
\Rightarrow ABCE là hình bình hành.
Lại có \angle ABC = {90^0};AB = BC = 2a
\Rightarrow ABCE là hình vuông \Rightarrow AC \bot BE.
Ta có \left\{ \begin{array}{l}BE \bot AC\,\,\,\left( {cmt} \right)\\BE \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BE \bot \left( {SAC} \right).
Mà BE \subset \left( {SBE} \right) \Rightarrow \left( {SAC} \right) \bot \left( {SBE} \right).
4) Ta có:
\begin{array}{l}AE \cap \left( {SCD} \right) = D\\ \Rightarrow \frac{{d\left( {E;\left( {SCD} \right)} \right)}}{{d\left( {A;\left( {SCD} \right)} \right)}} = \frac{{ED}}{{AD}} = \frac{1}{2}\\ \Rightarrow d\left( {E;\left( {SCD} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SCD} \right)} \right)\end{array}.
Trong \left( {SAC} \right) kẻ AH \bot SC\,\,\left( {H \in SC} \right).
Xét tam giác ACD có CE = \frac{1}{2}AD = 2a
\Rightarrow \Delta ACD vuông tại C \Rightarrow CD \bot AC.
Ta có \left\{ \begin{array}{l}CD \bot AC\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.
\Rightarrow CD \bot \left( {SAC} \right) \Rightarrow CD \bot AH
\left\{ \begin{array}{l}AH \bot CD\,\,\left( {cmt} \right)\\AH \bot SC\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right)
\Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH.
Trong tam giác vuông SAC:SA = \sqrt {S{C^2} - A{C^2}} = a\sqrt 2
Áp dụng hệ thức lượng trong tam giác vuông SAC ta có:
AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 2 .2\sqrt 2 a}}{{a\sqrt {10} }} = \frac{{2\sqrt {10} a}}{5}.
Vậy d\left( {E;\left( {SCD} \right)} \right) = \frac{1}{2}AH = \frac{{a\sqrt {10} }}{5}.

