Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình thoi cạnh \(a\) và có \(SA = SB = SC = a\). Chứng minh rằng:
a) Mặt phẳng \((ABCD)\) vuông góc với mặt phẳng \((SBD)\);
b) Tam giác \(SBD\) là tam giác vuông.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(AC \bot \left( {SBD} \right)\).
b) Chứng minh tam giác \(SBD\) có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó.
Lời giải chi tiết
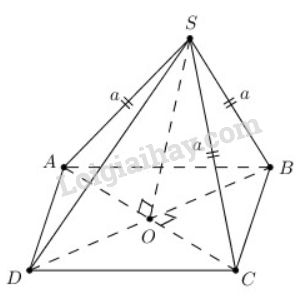
a) Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\)
Theo tính chất của hình thoi thì \(O\) là trung điểm của \(AC,BD\)
Xét tam giác cân \(SAC\) cân tại \(S\) ta có:
\(SO\) vừa là đường trung tuyến đồng thời là đường cao do đó \(SO \, \bot \, AC\) (1)
Mặt khác \(ABCD\) là hình thoi nên \(AC \, \bot \, BD\) (2)
Từ (1) và (2) suy ra \(AC\, \bot \, (SBD)\)
\(AC\subset (ABCD)\Rightarrow (ABCD) \, \bot \, (SBD)\)
b) \(∆SAC = ∆BAC (c.c.c)\)
Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau: \(SO = BO\)
\(O\) là trung điểm của \(BD\) nên \(OB=OD\)
\( \Rightarrow SO = BO = \dfrac{1}{2}BD\)
Tam giác \(SBD\) có trung tuyển \(SO = \dfrac{1}{2}BD\) nên vuông tại \(S\). (đpcm)
Cách khác:
Tam giác \(SOC\) vuông tại \(O\) nên theo Pi-ta-go ta có:
\(S{O^2} = S{C^2} - O{C^2} = {a^2} - O{C^2}\)
Tam giác \(BOC\) vuông tại \(O\) nên theo Pi-ta-go ta có:
\(B{O^2} = B{C^2} - O{C^2} = {a^2} - O{C^2}\)
\( \Rightarrow SO = BO = \dfrac{1}{2}BD\)
Tam giác \(SBD\) có trung tuyển \(SO = \dfrac{1}{2}BD\) nên vuông tại \(S\). (đpcm)

