Đề bài
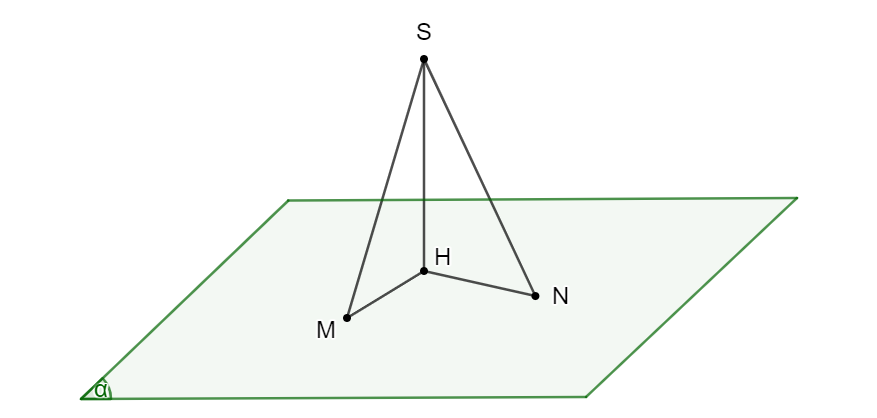
Cho điểm \(S\) không thuộc cùng mặt phẳng \((α)\) có hình chiếu là điểm \(H\). Với điểm \(M\) bất kì trên \((α)\) và \(M\) không trùng với \(H\), ta gọi \(SM\) là đường xiên và đoạn \(HM\) là hình chiếu của đường xiên đó. Chứng minh rằng:
a) Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh các tam giác vuông bằng nhau.
b) Sử dụng định lí Pytago.
Lời giải chi tiết
a) Gọi \(SN\) là một đường xiên khác.
\(SH \bot \left( \alpha \right) \Rightarrow \left\{ \begin{array}{l}
SH \bot HM\\
SH \bot HN
\end{array} \right.\)
\( \Rightarrow \Delta SHM,\Delta SHN\) vuông tại \(H\).
Xét hai tam giác vuông \(SHM\) và \(SHN\) có \(SH\) cạnh chung.
Nếu \(SM = SN \Rightarrow ∆SHM = ∆SHN \) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow HM = HN\).
Ngược lại nếu \(HM = HN\) thì \(∆SHM = ∆SHN \) (hai cạnh góc vuông)
\(\Rightarrow SM = SN\).
b) Xét tam giác vuông \(SHM\) và \(SHN\) có \(SH\) cạnh chung.
Giả sử \(SN > SM\)
Áp dụng định lí Pytago vào hai tam giác vuông \(SHM\) và \(SHN\) ta được:
\(\left\{ \begin{array}{l}H{N^2} = S{N^2} - S{H^2}\\H{M^2} = S{M^2} - S{H^2}\end{array} \right. \Rightarrow HN > HM\)
Phần đảo chứng minh tương tự
\(\left\{ \begin{array}{l}S{N^2} = H{N^2} + S{H^2}\\S{M^2} = H{M^2} + S{H^2}\end{array} \right. \Rightarrow SN > SM\)