Đề bài
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC=BD và AD=BC.
Video hướng dẫn giải
Lời giải chi tiết
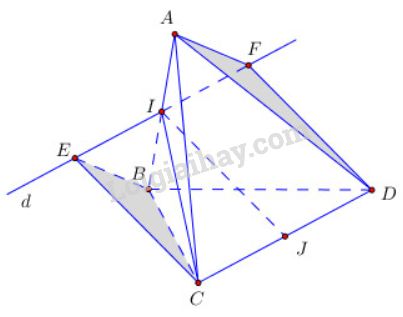
Gọi I,J lần lượt là trung điểm của AB,CD. Theo giả thiết IJ⊥AB,IJ⊥CD.
Qua I kẻ đường thẳng d//CD, lấy trên d điểm E,F sao cho IE=IF=CD2
Ta có IJ⊥CD(gt)⇒IJ⊥EF, lại có IJ⊥AB(gt)
⇒IJ⊥(AEBF).
Ta có CDFE là hình bình hành có IJ là đường trung bình
⇒CE//DF//IJ
⇒{CE⊥(AEBF)⇒CE⊥BEDF⊥(AEBF)⇒DF⊥AF
Ta có: ΔAIF=ΔBIE(c.g.c) suy ra: AF=BE
Xét ∆DFA và ∆CEB có:
+) ˆE=ˆF(=900)
+) AF=BE
+) DF=CE
⇒∆DFA=∆CEB(c.g.c)⇒AD=BC.
Chứng minh tương tự ta được BD=AC.

