Đề bài
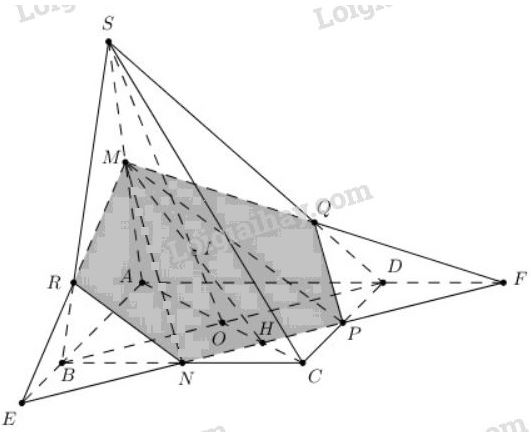
Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình bình hành. Gọi M,N,PM,N,P theo thứ tự là trung điểm của các đoạn thẳng SA,BC,CDSA,BC,CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)(MNP).
Gọi OO là giao điểm hai đường chéo của hình bình hành ABCDABCD, hãy tìm giao điểm của đường thẳng SOSO với mp(MNP)mp(MNP).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xác định giao tuyến của mặt phẳng (MNP)(MNP) với các mặt của hình chóp.
b) Tìm điểm chung của đường thẳng SOSO với mp(MNP)mp(MNP).
Lời giải chi tiết
a) Trong mặt phẳng (ABCD)(ABCD) kéo dài NPNP cắt đường thẳng AB,ADAB,AD lần lượt tại E,FE,F.
Trong mặt phẳng (SAD)(SAD) gọi Q=SD∩MFQ=SD∩MF
Trong mặt phẳng (SAB)(SAB) gọi R=SB∩MER=SB∩ME
Do đó
⇒{(MNP)∩(SAD)=MQ(MNP)∩(SDC)=QP(MNP)∩(ABCD)=PN(MNP)∩(SBC)=NR(MNP)∩(SAB)=RM
Từ đó ta có thiết diện là ngũ giác MQPNR.
b) Trong (ABCD) gọi H=AC∩NP
⇒H∈AC⊂(SAC)⇒MH⊂(SAC)
Trong (SAC), gọi I=SO∩MH⇒{I∈SOI∈MH⊂(MNP)
⇒I=SO∩(MNP).