Đề bài
Với giả thiết của bài tập 7, chu vi của thiết diện tính theo AM=xAM=x là:
(A) x(1+√3)x(1+√3); (B) 2x(1+√3)2x(1+√3);
(C) 3x(1+√3)3x(1+√3); (D) Không tính được.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lí Ta-let tính các cạnh của tam giác MNPMNP.
Lời giải chi tiết
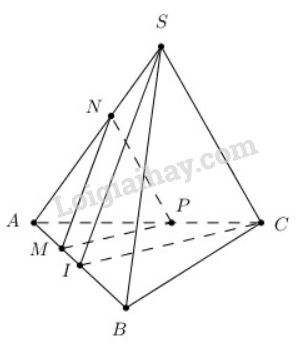
Tam giác ABCABC đều có II là trung điểm ABAB nên CI⊥ABCI⊥AB.
Tam giác AICAIC vuông tại II nên ⇒IC=ACsin600=a√32⇒IC=ACsin600=a√32
Ta có: MP//IC⇒AMAI=MPICMP//IC⇒AMAI=MPIC ⇒MP=AM.ICAI=x.a√32a2=x√3⇒MP=AM.ICAI=x.a√32a2=x√3
⇒MP=MN=x√3⇒MP=MN=x√3
Áp dụng định lí Ta-let trong tam giác SAC có NPSC=APAC=AMAINPSC=APAC=AMAI ⇒NP=SC.AMAI=a.xa2=2x
Vậy chu vi tam giác MNP là:
MN+MP+NP =x√3+x√3+2x =2x(1+√3)
Chọn đáp án B.

