Đề bài
Cho hình lăng trụ tam giác ABC.A′B′C′ có →AA′ = →a, →AB = →b, →AC = →c. Hãy phân tích (hay biểu thị véctơ →B′C, →BC′ qua các véctơ →a,→b, →c.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xen điểm thích hợp để làm xuất hiện các véc tơ →a,→b, →c, sử dụng các cặp vecto bằng nhau và bằng các vecto đã cho.
Lời giải chi tiết
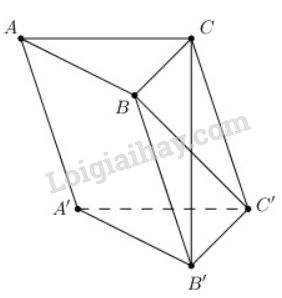
→B′C=→B′A′+→A′A+→AC=−→AB−→AA′+→AC=−→b−→a+→c→BC′=→BA+→AA′+→A′C′=−→AB+→AA′+→AC=−→b+→a+→c
Nhận xét: Ba véctơ →a;→b;→c ở trên gọi là bộ ba véctơ cơ sở (dùng để phân tích các véctơ khác).
Cách khác:
→B′C=→AC−→AB′=→AC−(→AB+→BB′)=→AC−→AB−→BB′=→AC−→AB−→AA′=→c−→b−→a→BC′=→AC′−→AB=→AA′+→A′C′−→AB=→AA′+→AC−→AB=→a+→c−→b

