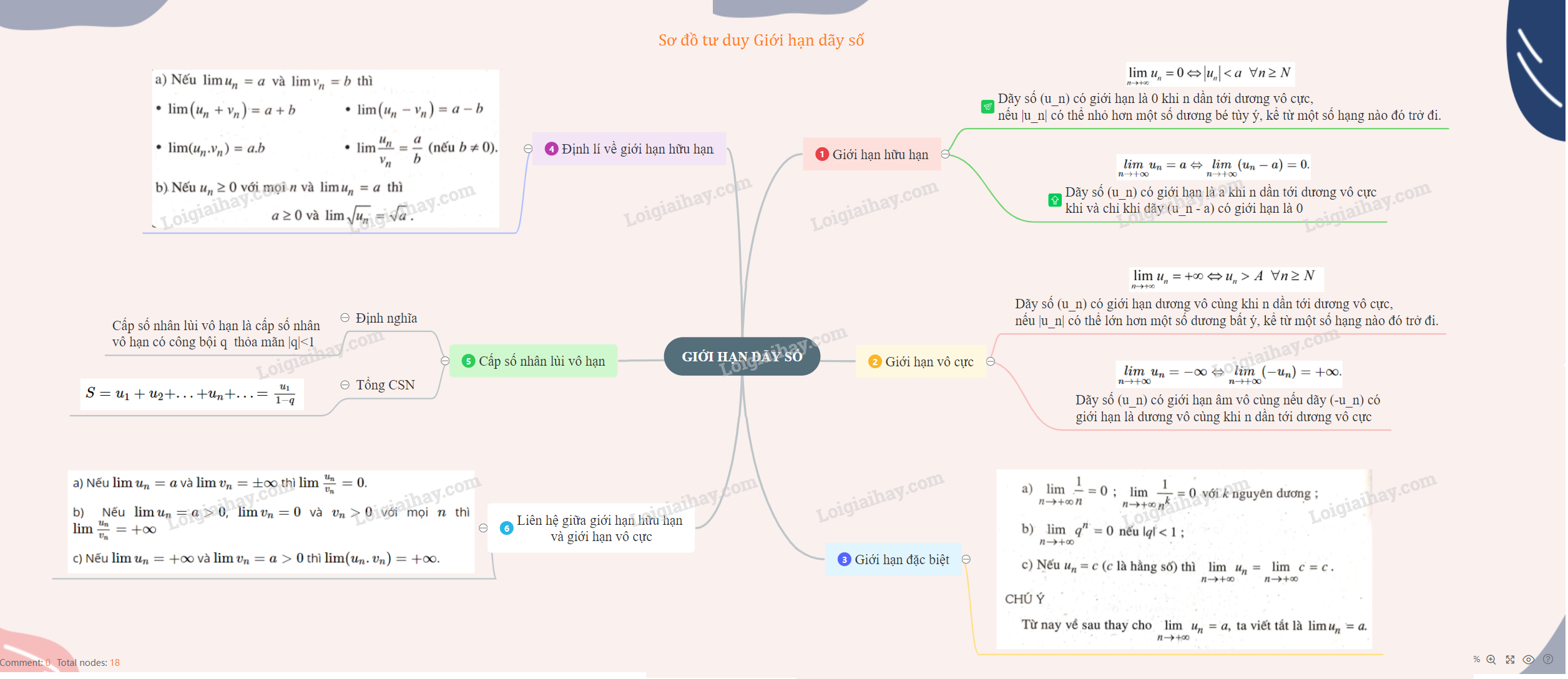
1. Giới hạn hữu hạn
+) limn→+∞un=0 khi và chỉ khi |un| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
+) limn→+∞un=a⇔limn→+∞(un−a)=0.
2. Giới hạn vô cực
+) limn→+∞un=+∞ khi và chỉ khi un có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
+ limn→+∞un=−∞⇔limn→+∞(−un)=+∞.
3. Các giới hạn đặc biệt
a) lim1n=0;
lim1nk=0;
limnk=+∞, với k nguyên dương.
b) limqn=0 nếu |q|<1;
limqn=+∞ nếu q>1.
c) limc=c (c là hằng số).
4. Định lí về giới hạn hữu hạn
a) Nếu limun=a và limvn=b, thì:
lim(un+vn)=a+b
lim(un−vn)=a−b
lim(un.vn)=ab
limunvn=ab (nếu b≠0).
b) Nếu un≥0 với mọi n và limun=a thì a>0 và lim√un=√a.
5. Định lí liên hệ giữa giới hạn hữu hạn và giới hạn vô cực.
a) Nếu limun=a và limvn=±∞ thì limunvn=0.
b) Nếu limun=a>0, limvn=0 và vn>0 với mọi n thì limunvn=+∞
c) Nếu limun=+∞ và limvn=a>0 thì lim(un.vn)=+∞.
6. Cấp số nhân lùi vô hạn
+ Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội q thỏa mãn |q|<1.
+) Công thức tính tổng S của cấp số lùi vô hạn (un):
S=u1+u2+...+un+...=u11−q