Đề bài
PHẦN 1: TRẮC NGHIỆM (3 điểm)
Câu 1: Lớp có 50 học sinh trong đó có 20 học sinh nữ. Chọn 3 bạn tham gia đội văn nghệ. Số cách chọn sao cho có ít nhất 1 bạn nam là:
A. C230.C120 B. C350−C320
C. C350−C330 D. C350.C330
Câu 2: Giá trị nhỏ nhất của hàm số y=3sin2x−2 bằng:
A. 4 B. 1
C. 5 D. −5
Câu 3: Trong mặt phẳng, biết V(O;k)(M)=M′. Chọn kết luận đúng.
A. →OM=k→OM′ B. →OM′=k→OM
C. →OM′=−k→OM D. →OM′=|k|→OM
Câu 4: Tập nghiệm của phương trình cosx=−√32 là:
A. x=±5π6+k2π,k∈Z
B. x=±2π3+k2π,k∈Z
C. x=±π3+k2π,k∈Z
D. x=±π6+kπ,k∈Z
Câu 5: Trong mặt phẳng tọa độ, cho M(−1;2), k=−12, V(O;k)(M)=M′, O là gốc tọa độ. Khi đó M′ có tọa độ là:
A. M′(−12;1) B. M′(1;−12) C. M′(12;−1) D. M′(−1;12)
Câu 6: Tập xác định của hàm số y=tan(x−π3) là:
A. D=R∖{±π3+kπ,k∈Z}
B. D=R∖{π3+k2π,k∈Z}
C. D=R∖{π3+kπ,k∈Z}
D. D=R∖{5π6+kπ,k∈Z}
Câu 7: Nghiệm của phương trình cos2x−cosx=0 thỏa mãn điều kiện −π<x<0 là:
A. x=π6 B. x=π4
C. x=−π2 D. x=π2
Câu 8: Tập nghiệm của phương trình √3sinx+cosx=0 là:
A. x=−π6+kπ,k∈Z B. x=−π3+k2π,k∈Z
C. x=−π3+kπ,k∈Z D. x=π3+kπ,k∈Z
Câu 9: Cho hình chóp S.ABCD có AC∩BD=M và AB∩CD=N. Giao tuyến của mặt phẳng (SAC) và mặt phẳng (SBD) là đường thẳng
A. SM B. SA C. MN D. SN
Câu 10: Trong mặt phẳng tọa độ, cho M(1;−2), phép tịnh tiến theo vectơ →v(−3;−3) biến điểm M thành điểm M′. Tọa độ điểm M′ là:
A. M′(2;−5) B. M′(4;−1)
C. M′(2;5) D. M′(−2;−5)
Câu 11: Trên giá sách có 7 quyển sách Toán khác nhau, 5 quyển Vật lí khác nhau, 8 quyển sách Hóa học khác nhau. Số cách chọn 1 quyển sách để đọc là:
A. 15 B. 13 C. 20 D. 280
Câu 12: Cho 5 chữ số 1, 2, 3, 5, 6. Lập các số tự nhiên gồm 3 chữ số đôi một khác nhau từ 5 chữ số đã cho. Tổng tất cả các số lập được bằng:
A. 22644 B. 24642 C. 26442 D. 44622
II. PHẦN TỰ LUẬN (7 điểm)
Câu 1 (2,0 điểm): Giải các phương trình sau:
a) 2sin(x−π6)−√3=0
b) sinx−√3cosx=−√2
Câu 2 (2,0 điểm):
a) Cho tập hợp A={1;2;3;4;5;6;7}. Từ A có thể lập đươc bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau?
b) Lớp 11A có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ?
Câu 3 (3 điểm):
1. Trong mặt phẳng Oxy , cho vectơ →v(2;−1) và đường thẳng x+y−3=0. Viết phương trình đường thẳng d′ là ảnh của đường thẳng d qua phép tịnh tiến theo →v.
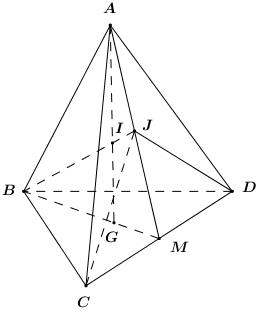
2. Cho tứ diện ABCD, gọi G là trọng tâm tam giác BCD, M là trung điểm của CD, I là điểm trên đoạn thẳng AG.
a) Xác định giao tuyến của mặt phẳng (ABG) và mặt phẳng (ACD).
b) Xác định giao điểm J của BI với mặt phẳng (ACD). Tính tỉ số giữa AI và AG để diện tích tam giác ACD bằng 2 lần diện tích tam giác JCD.
Lời giải chi tiết
PHẦN 1: TRẮC NGHIỆM (3 điểm)
| 1. B | 2. D | 3. B | 4. A | 5. C | 6. D |
| 7. C | 8. A | 9. A | 10. D | 11. C | 12. A |
Câu 1:
Phương pháp:
Sử dụng phần bù.
Cách giải:
Số cách chọn 3 bạn bất kì là: C350 cách.
Số cách chọn 3 bạn nữ là; C320 cách.
Vậy số cách chọn 3 bạn trong đó có ít nhất 1 bạn nam là: C350−C320 cách.
Chọn B.
Câu 2:
Phương pháp:
Sử dụng tính chất: −1≤sinα≤1∀α.
Cách giải:
Ta có:
−1≤sin2x≤1⇔−3≤3sin2x≤3⇔−5≤3sin2x−2≤1⇔−5≤y≤1
Vậy GTNN của hàm số bằng −5.
Chọn D.
Câu 3:
Phương pháp:
Sử dụng định nghĩa phép vị tự: V(O;k)(M)=M′⇔→OM′=k→OM.
Cách giải:
Ta có: V(O;k)(M)=M′⇔→OM′=k→OM.
Chọn B.
Câu 4:
Phương pháp:
Giải phương trình lượng giác cơ bản: cosx=cosα⇔x=±α+k2π(k∈Z).
Cách giải:
Ta có: cosx=−√32=cos5π6⇔x=±5π6+k2π(k∈Z).
Chọn A.
Câu 5:
Phương pháp:
Sử dụng định nghĩa phép vị tự: V(O;k)(M)=M′⇔→OM′=k→OM.
Cách giải:
Gọi M′(x′;y′)=V(O;−12)(M) ta có:
→OM′=−12→OM⇔{x′−xO=−12(xM−xO)y′−yO=−12(yM−yO)⇔{x′=−12.(−1)y′=−12.2⇔{x′=12y′=−1
Vậy M′(12;−1).
Chọn C.
Câu 6:
Phương pháp:
Hàm số y=tanα xác định ⇔α≠π2+kπ.
Cách giải:
Hàm số y=tan(x−π3) xác định ⇔x−π3≠π2+kπ⇔x≠5π6+kπ.
Vậy TXĐ của hàm số là D=R∖{5π6+kπ,k∈Z}.
Chọn C.
Câu 7:
Phương pháp:
- Đưa phương trình về dạng phương trình tích.
- Giải phương trình lượng giác cơ bản.
- Giải bất phương trình −π<x<0, tìm nghiệm x thỏa mãn.
Cách giải:
Ta có: cos2x−cosx=0⇔cosx(cosx−1)=0⇔[cosx=0cosx=1⇔[x=π2+kπx=π+k2π(k∈Z).
+ Xét họ nghiệm x=π2+kπ.
Cho −π<x<0⇔−π<π2+kπ<0⇔−32<k<−12.
Mà k∈Z⇒k=−1⇒x=−π2.
+ Xét họ nghiệm x=π+k2π.
Cho −π<π+k2π<0⇔−1<k<−12.
Mà k∈Z⇒k∈∅.
Vậy phương trình đã cho có duy nhất 1 nghiệm thỏa mãn là x=−π2.
Chọn C.
Câu 8:
Phương pháp:
- Chuyến vế, đưa về phương trình hàm tan.
- Giải phương trình lượng giác cơ bản: tanx=tanα⇔x=α+kπ(k∈Z).
Cách giải:
Ta có:
√3sinx+cosx=0⇔√3sinx=−cosx⇔tanx=−1√3⇔x=−π6+kπ(k∈).
Chọn A.
Câu 9:
Phương pháp:
Xác định hai điểm chung của hai mặt phẳng, từ đó xác định giao tuyến.
Cách giải:
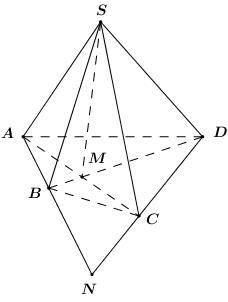
Xét (SAC) và (SBD) có:
+ S là điểm chung thứ nhất.
+ Trong (ABCD) ta có M=AC∩BD⇒{M∈AC⊂(SAC)M∈BD⊂(SBD) ⇒M∈(SAC)∩(SBD).
Vậy (SAC)∩(SBD)=SM.
Chọn A.
Câu 10:
Phương pháp:
Sử dụng định nghĩa phép tịnh tiến: T→u(M)=M′⇒→MM′=→u.
Cách giải:
Ta có: T→u(M)=M′⇒→MM′=→u
⇒{xM′=1+(−3)=−2yM′=−2+(−3)=−5.
Vậy M′(−2;−5).
Chọn D.
Câu 11:
Phương pháp:
- Tính số cách chọn 1 quyển sách Toán, 1 quyển sách Vật lí, 1 quyển sách Hóa.
- Sử dụng quy tắc cộng.
Cách giải:
Số cách chọn 1 quyển sách Toán là 7 cách.
Số cách chọn 1 quyển sách Vật lí là 5 cách.
Số cách chọn 1 quyển sách Hóa là 8 cách.
Áp dụng quy tắc cộng: Số cách chọn 1 quyển sách bất kì là: 7+5+8=20 cách.
Chọn C.
Câu 12:
Phương pháp:
- Sử dụng chỉnh hợp tính số cách chọn số có 3 chữ số đôi một khác nhau.
- Gọi số tự nhiên có 3 chữ số lập được là ¯abc.
- Số lần xuất hiện của mỗi số 1, 2, 3, 5, 6 ở mỗi vị trí a,b,c bằng số cách chọn ¯bc là A24=12 lần.
¯abc=a.102+b.101+c
Cách giải:
Từ 5 chữ số 1, 2, 3, 5, 6 ta lập được A35=60 số có 3 chữ số đôi một khác nhau.
Tổng các chữ số 1, 2, 3, 5, 6 là: 1+2+3+5+6=17.
Gọi số tự nhiên có 3 chữ số lập được là ¯abc.
- Trong 60 số lập được ở trên, số lần xuất hiện của mỗi số 1, 2, 3, 5, 6 ở mỗi vị trí a,b,c là A24=12 lần.
Chẳng hạn, số lần xuất hiện số 1 ở vị trí a bằng số cách chọn ¯bc từ 4 số 2,3,5,6 và bằng A24=12 lần, tương tự số 1 xuất hiện ở vị trí b A24=12 lần, ở vị trí c là A24=12 lần.
Vậy tổng của 60 số lập được là: 12.(1+2+3+5+6).(102+101+100)=22644.
Chọn A.
PHẦN II. TỰ LUẬN (7 điểm)
Câu 1:
Phương pháp:
a) Giải phương trình lượng giác cơ bản: sinx=sinα⇔[x=α+k2πx=π−α+k2π.
b) Giải phương trình dạng asinx+bcosx=c, chia cả 2 vế cho √a2+b2.
Cách giải:
a) 2sin(x−π6)−√3=0
⇔sin(x−π6)=√32⇔[x−π6=π3+k2πx−π6=2π3+k2π⇔[x=π2+k2πx=5π6+k2π(k∈Z)
Vậy nghiệm của phương trình là x = \dfrac{\pi }{2} + k2\pi ,\,\,x = \dfrac{{5\pi }}{6} + k2\pi .
b) \sin x - \sqrt 3 \cos x = - \sqrt 2
\begin{array}{l} \Leftrightarrow \dfrac{1}{2}\sin x - \dfrac{{\sqrt 3 }}{2}\cos x = - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin x\cos \dfrac{\pi }{3} - \cos x\sin \dfrac{\pi }{3} = - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x - \dfrac{\pi }{3}} \right) = - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x - \dfrac{\pi }{3} = - \dfrac{\pi }{4} + k2\pi \\x - \dfrac{\pi }{3} = \dfrac{{5\pi }}{4} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{19\pi }}{{12}} + k2\pi \end{array} \right.\end{array}
Vậy nghiệm của phương trình là x = \dfrac{\pi }{{12}} + k2\pi ;\,\,x = \dfrac{{19\pi }}{{12}} + k2\pi .
Câu 2:
Phương pháp:
a) Sử dụng chỉnh hợp.
b) Chia các trường hợp:
TH1: 3 học sinh nữ, 2 học sinh nam.
TH2: 4 học sinh nữ, 1 học sinh nam.
TH3: 5 học sinh nữ.
Cách giải:
a) Từ tập hợp A lập được A_7^4 = 840 số tự nhiên có 4 chữ số khác nhau.
b) Để chọn được 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ ta có các TH sau:
TH1: 3 học sinh nữ, 2 học sinh nam \Rightarrow Có C_{15}^3.C_{20}^2 = 86450.
TH2: 4 học sinh nữ, 1 học sinh nam \Rightarrow Có C_{15}^4.C_{20}^1 = 27300.
TH3: 5 học sinh nữ \Rightarrow Có C_{15}^5 = 3003.
Vậy có tất cả 86450 + 27300 + 3003 = 116753 cách.
Câu 3:
Phương pháp:
1. {T_{\overrightarrow v }}\left( d \right) = d' \Rightarrow d'//d, từ đó gọi phương trình đường thẳng d' có dạng theo phương trình đường thẳng d.
Lấy điểm A \in d bất kì. Tìm A' = {T_{\overrightarrow v }}\left( A \right).
Thay tọa độ điểm A' vào phương trình đường thẳng d'.
2. a) Xác định 2 điểm chung của hai mặt phẳng, từ đó xác định giao tuyến.
b) Xác định J là giao điểm của BI và một đường thẳng nằm trong \left( {ACD} \right).
Sử dụng định lí Menelaus để tính tỉ số.
Cách giải:
1. Vì {T_{\overrightarrow v }}\left( d \right) = d' \Rightarrow d'//d, do đó phương trình đường thẳng d' có dạng: d':\,\,x + y + c = 0\,\,\left( {c \ne - 3} \right).
Lấy A\left( {3;0} \right) \in d. Gọi A' = {T_{\overrightarrow v }}\left( A \right), khi đó ta có A'\left( {5; - 1} \right).
Vì {T_{\overrightarrow v }}\left( d \right) = d',\,\,A' = {T_{\overrightarrow v }}\left( A \right) \Rightarrow A' \in d'.
Suy ra 5 + \left( { - 1} \right) + c = 0 \Leftrightarrow c + 4 = 0 \Leftrightarrow c = - 4\,\,\left( {TM} \right).
Vậy phương trình đường thẳng d' là: x + y - 4 = 0.
2. a) Xét \left( {ABG} \right) và \left( {ACD} \right) có:
+ A là điểm chung thứ nhất.
+ Trong \left( {BCD} \right) ta có: M = BG \cap CD \Rightarrow \left\{ \begin{array}{l}M \in BG \subset \left( {ABG} \right)\\M \in CD \subset \left( {ACD} \right)\end{array} \right. \Rightarrow M \in \left( {ABG} \right) \cap \left( {ACD} \right).
Vậy \left( {ABG} \right) \cap \left( {ACD} \right) = AM.
b) Trong \left( {ABM} \right) gọi J = BI \cap AM ta có:
\left\{ \begin{array}{l}J \in BI\\J \in AM \subset \left( {ACD} \right) \Rightarrow J \in \left( {ACD} \right)\end{array} \right. \Rightarrow J = BI \cap \left( {ACD} \right).
Ta có: \dfrac{{{S_{JCD}}}}{{{S_{ACD}}}} = \dfrac{1}{2} = \dfrac{{JM}}{{AM}} \Rightarrow \dfrac{{JM}}{{JA}} = 1.
Áp dụng định lí Menelaus trong tam giác AGM ta có:
\dfrac{{BG}}{{BM}}.\dfrac{{JM}}{{JA}}.\dfrac{{IA}}{{IG}} = 1 \Leftrightarrow \dfrac{2}{3}.1.\dfrac{{IA}}{{IG}} = 2 \Leftrightarrow \dfrac{{IA}}{{IG}} = 3 \Rightarrow \dfrac{{AI}}{{AG}} = \dfrac{3}{4}.
Vậy để {S_{ACD}} = 2{S_{JCD}} thì \dfrac{{AI}}{{AG}} = \dfrac{3}{4}.

