Đề bài
Cho tam giác ABC. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B tỉ số 12 và phép đối xứng qua đường trung trực của BC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
B1: xác định ảnh của tam giác ABC qua phép vị tự
B2: xác định ảnh của tam giác ABC qua phép đối xứng
Lưu ý: để tìm ảnh của tam giác qua phép dời hình, ta tìm ảnh của từng đỉnh. Các đỉnh mới tạo thành ảnh của tam giác qua phép dời hình đó.
Lời giải chi tiết
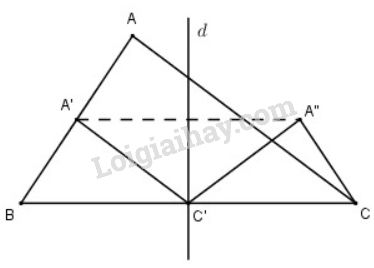
V(B;12)(A)=A′⇒→BA′=12→BA
⇒A′ là trung điểm của AB.
Tương tự ta có V(B;12)(C)=C′ thì C'\) là trung điểm của BC.
V(B;12)(B)=B
Do đó V(B;12)(ΔABC)=ΔA′BC′.
Dọi d là đường trung trực của BC. Khi đó,
Đd(B)=C; Đd(A′)=A″ ;Đd(C′)=C′
Nên phép đối xứng qua đường trung trực của BC biến ΔA′BC′ thành ΔA″CC′.
Vậy ảnh của tam giác ABC qua phép đồng dạng đã cho là tam giác A″CC′.

