Đề bài
Trên mặt phẳng (α) cho hình bình hành ABCD. Gọi O là giao điểm của AC và BD. S là một điểm nằm ngoài mặt phẳng (α) sao cho SA=SC,SB=SD. Chứng minh rằng:
a) SO⊥(α);
b) Nếu trong mặt phẳng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc mặt phẳng (SOH).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kết quả của định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải chi tiết
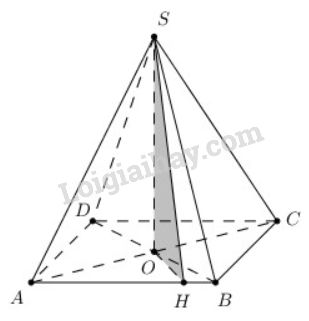
a) SA=SC⇒SAC cân tại S.
O là trung điểm của AC⇒SO là đường trung tuyến đồng thời là đường cao của tam giác cân nên SO⊥AC
Chứng minh tương tự ta có: SO⊥BD
Ta có:
SO⊥BDSO⊥ACBD∩AC={O}BD,AC⊂(ABCD)}⇒SO⊥(ABCD)
hay SO⊥mp(α).
b) SO⊥(ABCD)⇒SO⊥AB
{SO⊥ABSH⊥ABSO∩SH=SSO,SH⊂(SOH)⇒AB⊥(SOH)

