Đề bài
Trong mặt phẳng OxyOxy cho điểm I(1;1)I(1;1) và đường trong tâm II bán kính 22. Viết phương trình của đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm OO, góc 45∘45∘ và phép vị tự tâm OO, tỉ số √2√2.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Phép quay tâm OO, góc quay 450450 biến đường tròn tâm II bán kính RR thành đường tròn tâm I1I1 bán kính RR, với I1=Q(O;450)(I)I1=Q(O;450)(I).
Phép vị tự tâm OO, tỉ số √2√2 biến đường tròn tâm I1I1, bán kính RR thành đường tròn tâm I2I2; bán kính R2R2, với I2=V(O;√2)(I1);R2=√2RI2=V(O;√2)(I1);R2=√2R.
Lời giải chi tiết
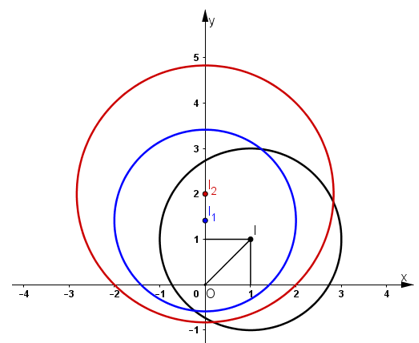
+ Gọi (I1;R1)=Q(O;45)(I;R)(I1;R1)=Q(O;45)(I;R) (Phép quay đường tròn tâm I,I, bán kính RR qua tâm OO một góc 450).450).
⇒{I1=Q(O;45)(I)R1=R
Xác định I1:
Ta có:
I1=Q(O;45)(I)⇒{OI1=OI^IOI1=45o⇒{OI1=OI=√12+12=√2^IOI1=45o⇔I1∈Oy⇒I1(0;√2)
+ Gọi I2(x″;y″)=V(O;√2)(I1) ta có:
→OI2=√2→OI1
⇔{x″=2.0=0y″=√2.√2=2
⇒I″(0;2)
Do đó phép vị tự tâm O, tỉ số √2 biến đường tròn tâm I1, bán kính R thành đường tròn tâm I2(0;2); bán kính R2=√2R=2√2.
Vậy phương trình đường tròn tâm I2, bán kính R2 là x2+(y−2)2=8.
Chú ý:
Cách khác để tìm I1 (chỉ dùng cho trắc nghiệm) như sau:
Gọi I1(x′;y′)=Q(I;450)(I) ta có:
{x′=1.cos45−1.sin45=0y′=1.sin45+1.cos45=√2 ⇒I1(0;√2)

