Đề bài
Cho hình bình hành \(ABCD\). Gọi \(Bx, Cy, Dz\) là các nửa đường thẳng song song với nhau lần lượt đi qua \(B, C, D\) và nằm về một phía của mặt phẳng \((ABCD)\) đồng thời không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng đi qua \(A\) và cắt \(Bx, Cy, Dz\) lần lượt tại \(B', C', D'\) với \(BB'=2, DD'=4\). Khi đó \(CC'\) bằng:
(A) 3 (B) 4
(C) 5 (D) 6
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kết quả của định lí: Cho hai mặt phẳng song song, nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau để chứng minh \(AB'C'D'\) là hình bình hành.
Gọi \(O,O'\) lần lượt là tâm của hình bình hành \(ABCD ,AB'C'D'\), dựa vào tính chất đường trung bình của hình thang và đường trung bình của tam giác để tính độ dài \(CC'\).
Lời giải chi tiết
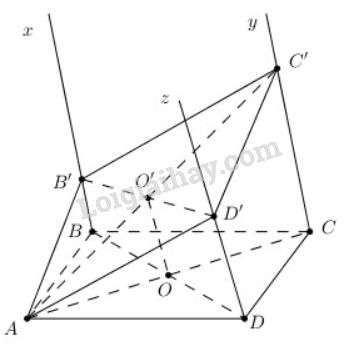
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BC//AD \Rightarrow BC//\left( {AD,Dz} \right)\\Bx//Dz\Rightarrow Bx//\left( {AD,Dz} \right)\end{array} \right. \\ \Rightarrow \left( {BC;Bx} \right)//\left( {AD;Dz} \right)\\\left\{ \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {BC;Bx} \right) = B'C'\\\left( {A'B'C'D'} \right) \cap \left( {AD;Dz} \right) = AD'\\\left( {BC,Bx} \right)//\left( {AD;Dz} \right)\end{array} \right. \end{array}\) \( \Rightarrow AD'//B'C' \)
Chứng minh tương tự ta có \(AB'//C'D'\). Do đó \(AB'C'D'\) là hình bình hành.
Gọi \(O,O'\) lần lượt là tâm của hình bình hành \(ABCD ,AB'C'D'\) ta có \(OO'\) là đường trung bình của hình thang \(BDD'B'\) nên \(BB'+DD'=2OO'\) (1).
\(OO'\) là đường trung bình của tam giác \(ACC'\) nên \(CC'=2OO'\) (2).
Từ (1) và (2) suy ra \(BB'+DD'=CC'\)
\(\Rightarrow CC'=2+4=6\)
Chọn đáp án D.

