Đề bài
PHẦN I. TRẮC NGHIỆM (5 điểm)
Câu 1 (NB): Giới hạn limx→1+2x−√x+3x+1 bằng:
A. +∞ B. 1
C. −∞ D. 0
Câu 2 (TH): Cho hàm số f(x)=x2+2x−2 . Giá trị f′(1) bằng
A. 5 B. −3
C. 4 D. −5
Câu 3 (TH): Giới hạn limx→−∞(x2−3x+1) bằng
A. +∞ B. −∞
C. −1 D. 1
Câu 4 (TH): Trong bốn giới hạn sau đây, giới hạn nào bằng 2?
A. limn+12n−1
B. lim1−4n2n+3
C. lim2n+3n−5
D. limn2+2n+3n2−2n+2
Câu 5 (TH): Cho hàm số y=x4−2x2−1 có đồ thị (C). Số tiếp tuyến song song với trục hoành của đồ thị (C) là
A. 1 B. 2
C. 3 D. 0
Câu 6 (VD): Hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB là tam giác đều cạnh a. Mặt phẳng (SAB) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng:
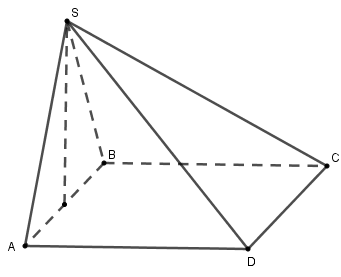
A. a B.a2
C. a√32 D. a√34
Câu 7 (VD): Nếu f(x)=xsinx thì f′(7π2) bằng
A. −1 B. 7π2
C. 1 D. 7π
Câu 8 (TH): Giới hạn limx→2018x2−2019x+2018x−2018 bằng
A. 2020 B. 2017
C. 2019 D. 2018
Câu 9 (TH): Đạo hàm của hàm số y=√sinx+2 bằng
A. y′=cosx√sinx+2
B. y′=−cosx2√sinx+2
C. y′=12√sinx+2
D. y′=cosx2√sinx+2
Câu 10 (VD): Giới hạn limx→0cos2018x−cos2019xx bằng
A. 0 B. +∞
C. −∞ D. 40372
Câu 11 (VD): Giả sử M là điểm có hoành độ x0=1 thuộc đồ thị hàm số (C) của hàm số y=x3−6x2+1. Khẳng định nào dưới đây đúng?
A. Tiếp tuyến của đồ thị (C) tại M có hệ số góc dương.
B. Góc giữa tiếp tuyến tại M và trục hoành bằng 600.
C. Đồ thị (C) không có tiếp tuyến tại M.
D. Tiếp tuyến của đồ thị (C) tại M vuông góc với đường thẳng (d):x−9y=0.
Câu 12 (TH): Với a và b là hai đường thẳng chéo nhau tùy ý, mệnh đề nào sau đây sai?
A. Tồn tại duy nhất một mặt phẳng (P) chứa b sao cho a⊥(P)
B. a và b là hai đường thẳng phân biệt
C. Tồn tại duy nhất một mặt phẳng (P) chứa b sao cho a//(P)
D. Nếu Δ là đường thẳng vuông góc chung của a và b thì Δ cắt cả hai đường thẳng a và b.
Câu 13 (VD): Cho hàm số f(x)={√x+3−2x2−1,x>1ax+2,x≤1. Giá trị của a để hàm số liên tục tại x=1 là
A. a=−178 B. a=158
C. a=−158 D. a=178
Câu 14 (VD): Cho hình chóp S.ABC,D là trung điểm của đoạn SA. Gọi h1;h2 lần lượt là khoảng cách từ S và D đến mặt phẳng (ABC). Tỉ số h1h2 bằng
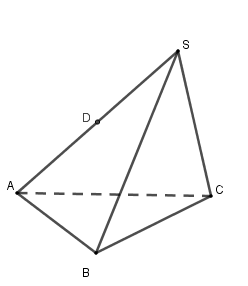
A. 13 B.3 C. 2 D. 12
Câu 15 (VD): Hình chóp đều S.ABCD có SA=AB=a. Cosin góc giữa hai mặt phẳng (SAB) và (SAD) bằng
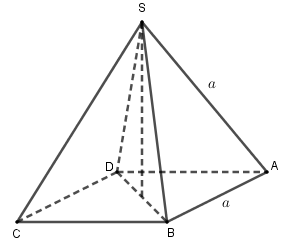
A. √22 B. −√22
C. 13 D. −13
Câu 16 (VD): Cho hàm số f(x)=1x2+1. Tập nghiệm của bất phương trình f′(x)>0 là
A. R B. ∅
C. (−∞;0) D. (0;+∞)
Câu 17 (VD): Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. M,N,P,Q lần lượt là trung điểm của AB,BC,C′D′ và D′A′. Khoảng cách giữa hai đường thẳng MN và PQ bằng
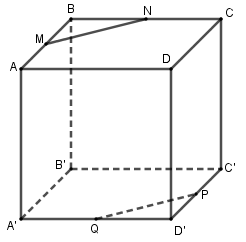
A. a B. a√22
C. a√62 D. a√2
Câu 18 (TH): Đạo hàm của hàm số y=sin(x3) là
A. y′=3x2sin(x3)
B. y′=3x2cos(x3)
C. y′=3cos(x2)
D. y′=3x2cos(x2)
Câu 19 (VD): Giới hạn lim12n−11n4n+4.12n+3 bằng
A. 112 B. 14
C. +∞ D. 0
Câu 20 (TH): Trong không gian cho hai đường thẳng a,b và mặt phẳng (P). Mệnh đề nào sau đây đúng?
A. Nếu a và b phân biệt, cùng song song với (P) thì a và b song song với nhau
B. Nếu b song song với (P) và a vuông góc với (P) thì a vuông góc với b
C. Nếu a và b cùng vuông góc với (P) thì a và b song song với nhau
D. Nếu b và (P) cùng vuông góc với a thì b song song với (P)
PHẦN II: TỰ LUẬN (5 điểm)
Câu 21 (VD) (1 điểm): Cho hàm số y=f(x)=2x+√3−x2. Giải phương trình f′(x)=0.
Câu 22 (VD) (1,5 điểm): Cho hàm số y=f(x)=−x4−x2+6. Viết phương trình tiếp tuyến của đồ thị hàm số biết rằng tiếp tuyến vuông góc với đường thẳng d:y=16x−1.
Câu 23 (VD) (2,5 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt phẳng đáy và AB=√3a,AD=a,SA=a.
a) Chứng minh tam giác SDC vuông.
b) Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
c) Tính theo a khoảng cách từ điểm C đến mặt phẳng (SBD).
Lời giải chi tiết
PHẦN I. TRẮC NGHIỆM (5 điểm)
| 1. D | 2. D | 3. A | 4.C | 5. B |
| 6. C | 7. A | 8. B | 9. D | 10. A |
| 11. D | 12. A | 13. C | 14. C | 15. C |
| 16. C | 17. C | 18. B | 19. B | 20. B |
Câu 1:
Phương pháp
Hàm số y=f(x) xác định tại x=x0 thì limx→x+0f(x)=f(x0).
Cách giải:
Ta có: limx→1+2x−√x+3x+1=2.1−√1+31+1=0.
Chọn D.
Câu 2:
Phương pháp
+) Tính f′(x) theo công thức (uv)′=u′v−v′uv2
+) Thay x=1 vào f′(x) để tính f′(1).
Cách giải:
Ta có f(x)=x2+2x−2 (ĐK: x≠2)
Suy ra f′(x)=(x2+2x−2)′
=(x2+2)′(x−2)−(x2+2)(x−2)′(x−2)2=2x(x−2)−(x2+2)(x−2)2
=2x2−4x−x2−2(x−2)2=x2−4x−2(x−2)2
Suy ra f′(1)=12−4.1−2(1−2)2=−5
Chọn D.
Câu 3:
Phương pháp
Đặt x2 làm nhân tử chung và tính các giới hạn.
Cách giải:
Ta có: limx→−∞(x2−3x+1)=limx→−∞[x2(1−3x+1x2)]
Vì limx→−∞x2=+∞ và limx→−∞(1−3x+1x2)=1 nên limx→−∞[x2(1−3x+1x2)]=+∞.
Vậy limx→−∞(x2−3x+1)=+∞.
Chọn A.
Câu 4:
Phương pháp
Tính từng giới hạn bằng cách chia cả tử và mẫu cho n (đối với A, B, C), chia tử và mẫu cho n2 (đối với câu D) rồi sử dụng giới hạn lim1n=0;lim1n2=0 để tính toán.
Cách giải:
+ Đáp án A : limn+12n−1=limnn+1n2nn−1n=lim1+1n2−1n=12≠2 nên loại A.
+ Đáp án B : lim1−4n2n+3=lim1n−4nn2nn+3n=lim1n−42+3n=−42=−2≠2 nên loại B.
+ Đáp án C : lim2n+3n−5=lim2nn+3nnn−5n=lim2+3n1−5n=21=2 nên chọn C.
+ Đáp án D : limn2+2n−3n2−2n+2=limn2n2+2nn−3n2n2n2−2nn2+2n2 =lim1+2n−3n21−2n+2n2=1≠2 nên loại D.
Chọn C.
Câu 5:
Phương pháp
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=x0 song song với trục hoành nếu có hệ số góc k=f′(x0)=0
Cách giải:
Ta có: y=x4−2x2−1⇒y′=4x3−4x.
Gọi M0(x0;y0) là tiếp điểm. Để tiếp tuyến tại M song song với trục hoành thì k=f′(x0)=0 ⇔4x30−4x0=0⇔4x0(x20−1)=0 ⇔[x0=0x0=±1 .
Với x0=0⇒y0=−1 ta có điểm M(0;−1).
⇒ Tiếp tuyến của đồ thị hàm số tại M(0;−1) có phương trình y=0(x−0)−1 hay y=−1.
Với x0=−1⇒y0=−2 ta có điểm M(−1;−2).
⇒ Tiếp tuyến của đồ thị hàm số tại M(−1;−2) có phương trình y=0(x+1)−2 hay y=−2.
Với x0=1⇒y0=−2 ta có điểm M(1;−2).
⇒ Tiếp tuyến của đồ thị hàm số tại M(1;−2) có phương trình y=0(x−1)−2 hay y=−2.
Do đó có 2 tiếp tuyến cần tìm là y=−1 và y=−2.
Chọn B.
Chú ý khi giải :
Một số em sau khi tính ra 3 giá trị x0 mà không viết phương trình tiếp tuyến rồi chọn ngay đáp án C là sai. Cần chú ý kiểm tra, ở đây hai tiếp tuyến tại các điểm (1;−2) và (−1;−2) là trùng nhau.
Câu 6:
Phương pháp
Ta sử dụng kiến thức {(P)⊥(Q)(P)∩(Q)=aa⊥d,a⊂(P)⇒a⊥(Q) để tìm chiều cao hình chóp
Chỉ ra BC⊥(SAB) rồi xác định đoạn vuông góc chung của SA và BC.
Từ đó khoảng cách giữa SA và BC là đoạn BK với BK⊥SA tại K.
Cách giải:
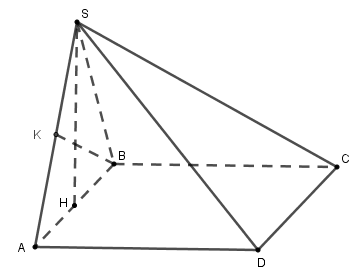
Gọi H là trung điểm đoạn AB. Khi đó SH⊥AB (do tam giác SAB đều)
Lại có {(SAB)⊥(ABC)(gt)(SAB)∩(ABC)=BASH⊥AB(cmt);SH⊂(SAB)⇒SH⊥(ABC)⇒SH⊥BC
Mà BC⊥AB (do ABCD là hình vuông) nên BC⊥(SAB)
Trong tam giác SAB, lấy K là trung điểm SA⇒BK⊥SA (do tam giác SAB đều)
Ta có {BC⊥BK(doBC⊥(SAB))BK⊥SA nên BK là đoạn vuông góc chung của SA và BC
Mà BK là đường trung tuyến trong tam giác SAB đều cạnh a nên BK=a√32
Hay khoảng cách giữa SA và BC là BK=a√32.
Chọn C.
Câu 7:
Phương pháp
- Tính f′(x), sử dụng công thức đạo hàm của một tích (uv)′=u′v+uv′ và công thức tính đạo hàm các hàm số cơ bản.
- Thay x=7π2 vào tính f′(7π2).
Cách giải:
f(x)=xsinx
⇒f′(x)=(xsinx)′=(x)′sinx+x(sinx)′ =sinx+xcosx
Do đó f′(7π2)=sin7π2+7π2.cos7π2=−1+7π2.0=−1 .
Chọn A.
Câu 8:
Phương pháp
Phân tích tử thức thành nhân tử để khử dạng vô định
Cách giải:
Ta có limx→2018x2−2019x+2018x−2018=limx→2018(x−2018)(x−1)x−2018 =limx→2018(x−1) =2018−1=2017
Chọn B.
Câu 9:
Phương pháp
Đạo hàm hàm hợp (√u)′=u′2√u.
Cách giải:
Ta có: y′=(√sinx+2)′=(sinx+2)′2√sinx+2 =cosx2√sinx+2
Chọn D.
Câu 10:
Phương pháp
Sử dụng công thức cosa−cosb=−2(sin(a+b2)−sin(a−b2)) và công thức limx→0sinxx=1 để khử dạng vô định.
Cách giải:
Ta có limx→0cos2018x−cos2019xx
=limx→0−2sin4037x2.sin(−x2)x
=limx→0(sin4037x2).limx→0sinx2x2
=0.1=0
Chọn A.
Câu 11:
Phương pháp
- Viết phương trình tiếp tuyến của đồ thị hàm số tại M theo công thức y=f′(x0)(x−x0)+y0.
- Nhận xét tính đúng sai của từng đáp án và kết luận.
Cách giải:
Ta có: M(1;−4), y′=3x2−12x⇒y′(1)=3.12−12.1=−9 .
Tiếp tuyến của đồ thị hàm số tại M(1;−4) có phương trình:
y=y′(1)(x−1)−4=−9(x−1)−4 hay y=−9x+5.
+ Hệ số góc k=−9<0 nên A sai.
+ Góc tạo bởi tiếp tuyến với Ox thỏa mãn tanα=−9⇔α≈96020′ nên B sai.
+ Đáp án C sai.
+ (d):x−9y=0 ⇔y=19x có hệ số góc k=19.
Dễ thấy 19.(−9)=−1 nên tiếp tuyến vuông góc với (d).
Chọn D.
Câu 12:
Phương pháp
Nhận xét tính đúng sai của từng đáp án, sử dụng lý thuyết hai đường thẳng chéo nhau.
Cách giải:
Đáp án A: Giả sử a,b chéo nhau tùy ý và tồn tại mặt phẳng (P) chứa b và a⊥(P).
Khi đó a⊥b. Diều này chưa chắc đúng do giả thiết chưa cho a⊥b nên A sai.
Chọn A.
Câu 13:
Phương pháp
Hàm số y=f(x) liên tục tại x=x0 ⇔limx→x0f(x)=f(x0).
Cách giải:
Ta có: f(1)=a+2.
+) limx→1−f(x)=a+2.
+) limx→1+f(x)=limx→1+√x+3−2x2−1=limx→1+x+3−4(x2−1)(√x+3+2) =limx→1+x−1(x2−1)(√x+3+2) =limx→1+1(x+1)(√x+3+2) =1(1+1)(√1+3+2)=18
⇒limx→1+f(x)=18
Hàm số liên tục tại x = 1 \Leftrightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right) \Leftrightarrow a + 2 = \frac{1}{8} \Leftrightarrow a = - \frac{{15}}{8}.
Chọn C.
Câu 14:
Phương pháp :
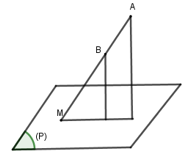
Sử dụng tỉ lệ khoảng cách:
Nếu đường thẳng AB cắt mặt phẳng \left( P \right) tại M thì ta có \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}} = \frac{{AM}}{{BM}}
Cách giải:
Ta có đường thẳng SD cắt mặt phẳng \left( {ABC} \right) tại A nên \frac{{d\left( {S;\left( {ABC} \right)} \right)}}{{d\left( {D;\left( {ABC} \right)} \right)}} = \frac{{SA}}{{DA}} = 2
Hay \frac{{{h_1}}}{{{h_2}}} = 2.
Chọn C.
Câu 15:
Phương pháp
Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
Cách giải:
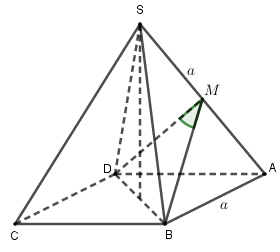
Gọi M là trung điểm của SA.
Do S.ABCD đều nên SA = SB = SC = SD. Mà SA = AB = a nên các tam giác SAB,SAD là tam giác đều.
Khi đó BM \bot SA,DM \bot SA.
Ta có: \left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\BM \subset \left( {SAB} \right),DM \subset \left( {SAD} \right)\\BM \bot SA,DM \bot SA\end{array} \right. \Rightarrow góc giữa \left( {SAB} \right) và \left( {SAD} \right) bằng \widehat {\left( {BM,DM} \right)} = \alpha .
Dễ thấy BM = DM = \frac{{a\sqrt 3 }}{2},BD = a\sqrt 2 .
\Rightarrow \cos \widehat {BMD} = \frac{{B{M^2} + D{M^2} - B{D^2}}}{{2BM.DM}} = \frac{{\frac{{3{a^2}}}{4} + \frac{{3{a^2}}}{4} - 2{a^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = - \frac{1}{3}.
\Rightarrow \cos \alpha = \frac{1}{3}
Chọn C.
Câu 16:
Phương pháp
Tính f'\left( x \right) theo công thức {\left( {\frac{1}{u}} \right)^\prime } = - \frac{{u'}}{{{u^2}}}
Rồi giải bất phương trình f'\left( x \right) > 0
Cách giải:
TXĐ: D = \mathbb{R}
Ta có f'\left( x \right) = {\left( {\frac{1}{{{x^2} + 1}}} \right)^\prime } = - \frac{{2x}}{{{{\left( {{x^2} + 1} \right)}^2}}}
Xét f'\left( x \right) > 0 \Leftrightarrow \frac{{ - 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0 \Leftrightarrow - 2x > 0 \Leftrightarrow x < 0
Vậy S = \left( { - \infty ;0} \right)
Chọn C.
Câu 17:
Phương pháp
- Chứng minh MN//PQ và MN \bot MQ.
- Từ đó suy ra d\left( {MN,PQ} \right) = MQ và tính toán.
Cách giải:
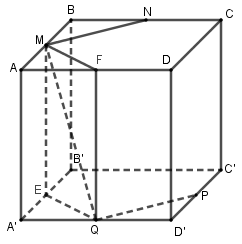
Dễ thấy MN//AC//A'C'//PQ.
Gọi E,F lần lượt là trung điểm A'B',AD.
Khi đó MN \bot ME (vì ME \bot \left( {ABCD} \right)).
Mà MN \bot MF (tính chất trung điểm các cạnh hình vuông).
Do đó MN \bot \left( {MEQF} \right) \Rightarrow MN \bot MQ nên d\left( {MN,PQ} \right) = d\left( {Q,MN} \right) = QM.
Tam giác MEQ vuông tại E có ME = a,EQ = \frac{1}{2}B'D' = \frac{{a\sqrt 2 }}{2} nên QM = \sqrt {M{E^2} + E{Q^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{2}} = \frac{{a\sqrt 6 }}{2}
Vậy d\left( {MN,PQ} \right) = \frac{{a\sqrt 6 }}{2}.
Chọn C.
Câu 18:
Phương pháp
Sử dụng công thức {\left( {\sin u} \right)^\prime } = u'\cos u
Cách giải:
Ta có y' = {\left( {\sin \left( {{x^3}} \right)} \right)^\prime } = {\left( {{x^3}} \right)^\prime }\cos \left( {{x^3}} \right) = 3{x^2}\cos \left( {{x^3}} \right)
Chọn B.
Câu 19:
Phương pháp
Chia cả tử và mẫu cho {12^n} và sử dụng giới hạn \lim {\left| q \right|^n} = 0 với 0 < \left| q \right| < 1.
Cách giải:
Ta có: \lim \frac{{{{12}^n} - {{11}^n}}}{{{4^n} + {{4.12}^n} + 3}} = \lim \frac{{1 - {{\left( {\frac{{11}}{{12}}} \right)}^n}}}{{{{\left( {\frac{1}{3}} \right)}^n} + 4 + \frac{3}{{{{12}^n}}}}} = \frac{{1 - 0}}{{0 + 4 + 0}} = \frac{1}{4}.
Chọn B.
Câu 20:
Phương pháp
Sử dụng lý thuyết về quan hệ song song và vuông góc của đường thẳng và mặt phẳng trong không gian
Cách giải:
Đáp án A : Sai vì có thể xảy ra trường hợp a,b cắt nhau (cùng nằm trong mặt phẳng song song \left( P \right)) hoặc có thể chéo nhau.
Đáp án B : Đúng.
Đáp án C : Sai vì có thể xảy ra trường hợp a,b trùng nhau.
Đáp án D : Sai vì có thể xảy ra trường hợp b \subset \left( P \right).
Chọn B.
PHẦN II: TỰ LUẬN (5 điểm)
Câu 21:
Phương pháp:
Tính f'\left( x \right) rồi giải phương trình f'\left( x \right) = 0.
Sử dụng công thức đạo hàm {\left( {\sqrt u } \right)^\prime } = \frac{{u'}}{{2\sqrt u }}
Cách giải:
ĐK : - \sqrt 3 \le x \le \sqrt 3
Ta có f'\left( x \right) = 2 + \frac{{ - 2x}}{{2\sqrt {3 - {x^2}} }} = 2 - \frac{x}{{\sqrt {3 - {x^2}} }}
Xét f'\left( x \right) = 0 \Leftrightarrow 2 - \frac{x}{{\sqrt {3 - {x^2}} }} = 0
\begin{array}{l} \Rightarrow 2\sqrt {3 - {x^2}} = x\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\4\left( {3 - {x^2}} \right) = {x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\5{x^2} = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\left[ \begin{array}{l}x = \sqrt {\frac{{12}}{5}} \\x = - \sqrt {\frac{{12}}{5}} \end{array} \right.\end{array} \right.\\ \Rightarrow x = \frac{{2\sqrt {15} }}{5}\,\left( {TM} \right)\end{array}
Vậy x = \frac{{2\sqrt {15} }}{5}.
Câu 22:
Phương pháp
Xác định hệ số góc k của tiếp tuyến. Sử dụng hai đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng - 1.
Từ đó giải phương trình f'\left( x \right) = k để tìm hoành độ tiếp điểm
Viết phương trình tiếp tuyến có hệ số góc k và đi qua điểm có tọa độ \left( {{x_0};{y_0}} \right) là
y = k\left( {x - {x_0}} \right) + {y_0}
Cách giải:
Ta có y' = - 4{x^3} - 2x. Gọi hệ số góc của tiếp tuyến là k.
Vì tiếp tuyến song song với đường thẳng y = \frac{1}{6}x - 1 nên ta có k.\frac{1}{6} = - 1 \Leftrightarrow k = - 6
Hoành độ tiếp điểm của tiếp tuyến và đồ thị hàm số là nghiệm của phương trình y' = - 6
\Leftrightarrow - 4{x^3} - 2x = - 6 \Leftrightarrow 4{x^3} + 2x - 6 = 0 \Rightarrow x = 1 \Rightarrow y = 4
Phương trình tiếp tuyến cần tìm là y = - 6\left( {x - 1} \right) + 4 \Leftrightarrow y = - 6x + 10
Câu 23:
Phương pháp
a) Chứng minh CD \bot \left( {SAD} \right) suy ra kết luận.
b) Chứng minh CB \bot \left( {SAB} \right) suy ra góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng nằm trong hai mặt phẳng và vuông góc với giao tuyến.
c) Sử dụng phương pháp tính gián tiếp:
\frac{{d\left( {A,\left( \alpha \right)} \right)}}{{d\left( {H,\left( \alpha \right)} \right)}} = \frac{{IA}}{{IH}} \Rightarrow {\rm{ }}d\left( {A,\left( \alpha \right)} \right) = \frac{{IA}}{{IH}}.d\left( {H,\left( \alpha \right)} \right)
Chú ý: Nếu tứ diện OABC có OA,OB,OC đôi một vuông góc và có đường cao OH thì \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}.
Cách giải:
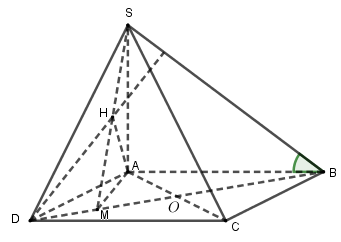
a) Ta có: \left\{ \begin{array}{l}SA \bot \left( {ABCD} \right)\\CD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow SA \bot CD.
Mà CD \bot AD nên CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD.
Do đó tam giác SCD vuông tại D.
b) Ta có: \left. \begin{array}{l}SA \bot \left( {ABCD} \right)\\BC \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow SA \bot BC.
Mà BC \bot AB nên BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB.
Lại có \left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SB \subset \left( {SBC} \right),AB \subset \left( {ABCD} \right)\\SB \bot BC,AB \bot BC\end{array} \right. nên góc giữa hai mặt phẳng \left( {SBC} \right) và \left( {ABCD} \right) là góc giữa hai đường thẳng SB và AB hay \widehat {SBA}.
Tam giác SAB vuông tại A có \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {SBA} = {30^0}
Vậy góc giữa hai mặt phẳng \left( {SBC} \right) và \left( {ABCD} \right) bằng {30^0}.
c) Gọi O = AC \cap BD \Rightarrow AC \cap \left( {SBD} \right) = O
Mà AO = CO nên d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right).
Dễ thấy tứ diện SABD có ba cạnh AB,AD,AS đôi một vuông góc nên gọi H là hình chiếu của A lên \left( {SBD} \right) thì:
\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{S^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{7}{{3{a^2}}} \Rightarrow A{H^2} = \frac{{3{a^2}}}{7} \Rightarrow AH = \frac{{a\sqrt {21} }}{7}.
Vậy d\left( {C,\left( {SBD} \right)} \right) = \frac{{a\sqrt {21} }}{7}.
Chú ý khi giải:
Trường hợp HS không được học công thức \frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{S^2}}} thì có thể chứng minh như sau:
Gọi H là trực tâm của tam giác SBD và M = SH \cap BD thì SH \bot BD. Mà SA \bot BD nên BD \bot \left( {SAH} \right) \Rightarrow BD \bot AH và BD \bot AM.
Tương tự chứng minh được SB \bot AH hay AH \bot \left( {SBD} \right).
Xét tam giác vuông SAM có \frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{M^2}}}.
Xét tam giác vuông ABD có \frac{1}{{A{M^2}}} = \frac{1}{{A{D^2}}} + \frac{1}{{A{B^2}}}.
Vậy \frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{S^2}}} (đpcm).

