Đề bài
A. Câu hỏi trắc nghiệm (4,0 điểm) Chọn phương án đúng
Câu 1 : Hàm số nào sau đây tuần hoàn với chu kì T=π?
A. y=sinx
B. y=2sinx
C. y=sin2x
D. y=2+sinx
Câu 3 : Tập xác định của hàm số y=√sinx−1 là:
A. R
B. {kπ|k∈Z}
C. {π2+k2π|k∈Z}
D. {π2+kπ|k∈Z}
Câu 4 : Số nghiệm của phương trình cos2x+1=0 trên đoạn [0;1000π] là:
A. 1000
B. 999
C. 2000
D. 1001
Câu 5 : Tập giá trị của tham số m để phương tình 2sin(x+2017π2)+3m=0 có nghiệm là:
A. (−1;1)
B. [−1;1]
C. [−32;32]
D. [−23;23].
Câu 6 : Cho hàm số y=sinx−cosx+√2sinx+cosx+2. Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là N. Khi đó giá trị của 2M+N là:
A. 4√2
B. 2√2
C. 4
D. √2
Câu 7 : Biết A2n+C3n=50(n∈N∗). Khi đó giá trị của n là:
A. 4
B. 5
C. 6
D. 7
Câu 8 : Hệ số của số hạng chứa x6 trong khai triển Newton (x−2x2)15 là:
A. −3640
B. 3640
C. 455
D. −1863680
Câu 9 : Một lớp có 30 học sinh gồm 20 nam, 10 nữ. Hỏi có bao nhiêu cách chọn một nhóm 3 học sinh sao cho nhóm đó có ít nhất 01 học sinh là nữ.
A. 1140
B. 2920
C. 1900
D. 900
Câu 10 : Từ các số 0; 1; 2; 3; 4; 5; 6; 7 lập được bao nhiêu số có 6 chữ số mà chữ số liền sau nhỏ hơn số liền trước?
A. 7
B. 20160
C. 5040
D. 28
Câu 11 : Một đề trắc nghiệm có 50 câu hỏi gồm 20 câu mức độ nhận biết, 20 câu mức độ vận dụng và 10 câu mức độ vận dụng cao. Xác suất để bạn An làm hết 20 cấu mức độ nhận biết là 0,9; 20 câu mức độ vận dụng là 0,8 và 10 câu mức độ vận dụng cao là 0,6. Xác suất để bạn An làm trọn vạn 50 câu là:
A. 0,432
B. 0,008
C. 0,228
D. 1
Câu 12 : Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm A(1;5);B(−3;2). Biết các điểm A, B theo thứ tự là ảnh của các điểm M, N qua phép vị tự tâm O tỉ số k=−2. Độ dài đoạn thẳng MN là:
A. 50
B. 12,5
C. 10
D. 2,5
Câu 13 : Trong mặt phẳng Oxy, cho đường tròn (C):(x−1)2+(y+2)2=9 và đường tròn (C′):(x+1)2+(y−3)2=9. Phép tịnh tiến theo vecto →v biến đường tròn (C) thành đường tròn (C′). Khi đó vecto →v có tọa độ là:
A. →v(5;2)
B. →v(2;−5)
C. →v(−2;5)
D. →v(2;5)
Câu 14 : Chọn mệnh đề đúng trong các mệnh đề sau:
A. Ba đường thẳng đôi một song song thì chúng nằm trên cùng một mặt phẳng.
B. Ba đường thẳng phân biệt đôi một cắt nhau thì chúng nằm trên cùng một mặt phẳng.
C. Ba đường thẳng đôi một cắt nhau thì chúng đồng quy tại 1 điểm.
D. Cả A, B, C đều sai.
Câu 15 : Cho tứ diện ABCD có M, N theo thứ tự là trung điểm của AB, BC. Gọi P là điểm thuộc cạnh CD sao cho CP=2PD và Q là điểm thuộc cạnh AD sao cho bốn điểm M, N, P, Q đồng phẳng. Khẳng định nào sau đây là đúng?
A. Q là trung điểm của đoạn thẳng AC
B. DQ=2AQ
C. AQ=2DQ
D. AQ=3DQ
Câu 16 : Cho hình chóp S.ABCD. Một mặt phẳng (P) bất kì cắt các cạnh SA, SB, SC và SD lần lượt tại A’, B’, C’, D’. Gọi I là giao điểm của AC và BD. Chọn khẳng định đúng trong các khẳng định dưới đây?
A. Các đường thẳng AB, CD, C’D’ đồng quy
B. Các đường thẳng AB,CD, A’B’ đồng quy
C. Các đường thẳng A’C’, B’D’, SI đồng quy
D. Các phương án A, B, C đều sai.
B. Câu hỏi tự luận (6,0 điểm)
Câu 1 (1,5 điểm – 1,0 điểm) Giải các phương trình sau:
1) sinx−√3cos(x+π)=2sin2x
2) 5sin2x−2sin2x+7cos2x=4
Câu 2 (1,5 điểm – 1,5 điểm)
1. Cho n là số tự nhiên thỏa mãn C0n+2C1n+22C2n+...+2nCnn=59049. Biết số hạng thứ 3 trong khai triển Newton của (x2−3x)n có giá trị bằng 812n. Tìm x?
2. Có 2 lô sản phẩm. Lô I có 10 sản phẩm tốt và 5 sản phẩm xấu. Lô II có 12 sản phẩm tốt và 3 sản phẩm xấu. Một người chọn ngẫu nhiên ra 2 sản phẩm từ lô I và 2 sản phẩm từ lô II một cách độc lập. Tính xác suất để cả 4 sản phẩm được chọn ra đều là sản phẩm tốt.
Câu 3 (3,0 điểm – 3,0 điểm: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi M, N theo thứ tự là trọng tâm của các tam giác SAB và SCD.
a) Chứng minh rằng MN song song với mặt phẳng (ABCD).
b) Gọi I là giao điểm của các đường thẳng BM và CN. Chứng minh rằng SI // CD và tính tỉ số SICD.
c) Gọi G là giao điểm của đường thẳng MN với mặt phẳng (SAC). Chứng minh rằng G là trọng tâm tam giác SBD.
Câu 4 (0 điểm – 0,5 điểm): Một đề thi trắc nghiệm gồm 50 câu hỏi độc lập. Mỗi câu hỏi có 4 đáp án trả lời trong đó chỉ có 1 đáp án đúng. Mỗi câu trả lời đúng được 0,2 điểm, câu trả lời sai được 0 điểm. Học sinh A làm bài bằng cách chọn ngẫu nhiên câu trả lời cho tất cả 50 câu hỏi. Biết xác suất làm đúng câu k của học sinh A đạt giá trị lớn nhất. Tìm k và số điểm học sinh A đạt được khi đó.
Lời giải chi tiết
A. Câu hỏi trắc nghiệm
| 1. C | 2. B | 3. C | 4. A | 5. D |
| 6. A | 7. C | 8. A | 9. B | 10. D |
| 11. A | 12. D | 13. C | 14. D | 15. C |
| 16. C |
|
|
|
|
B. Câu hỏi tự luận
Câu 1.
1)
1)sinx−√3cos(x+π)=2sin2x⇔sinx+√3cosx=2sin2x⇔12sinx+√32cosx=sin2x⇔sinxcosπ3+cosxsinπ3=sin2x⇔sin(x+π3)=sin2x⇔[x+π3=2x+k2πx+π3=π−2x+k2π⇔{x=π3+k2πx=2π9+k2π3(k∈Z)
Vậy x∈{π3+k2π;2π9+k2π3|k∈Z}
2) 5sin2x−2sin2x+7cos2x=4
⇔5sin2x−4sinxcosx+7cos2x=4
TH1: cosx=0⇔sin2x=1
⇔5=4 (Vô nghiệm)
TH2: cosx≠0⇔x≠π2+kπ
Chia cả 2 vế của phương trình cho cos2x ta được:
5tan2x−4tanx+7=4(1+tan2x)⇔tan2x−4tanx+3=0⇔[tanx=1tanx=3⇔[x=π4+kπx=arctan3+kπ(k∈Z)(tm)
Vậy x∈{π4+kπ;arctan3+kπ|k∈Z}.
Câu 2:
1.
Xét tổng (x+2)n=n∑k=0Cknxn−k2k=C0n.xn+C1nxn−121+C2nxn−222+...+Cnn2n
Thay x = 1 ta có: 3n=C0n+2C1n+22C2n+...+2nCnn=59049
⇒n=10
Ta có: (x2−3x)10=10∑k=0Ck10(x2)10−k(−3x)k=10∑k=0Ck10x20−2k(−3)kx−k=10∑k=0Ck10(−3)kx20−3k
Số hạng thứ 3 trong khai triển trên là C210(−3)2.x14=812n=812.10=405
⇔405.x14=405⇔x=±1
Vậy x=1 hoặc x=−1.
2. Số cách chọn 4 sản phẩm bất kì (2sp lô I + 2sp lô II) là C215.C215 cách ⇒n(Ω)=C215.C215
Số cách chọn 2 sản phẩm tốt từ lô I là C210=45
Số cách chọn 2 sản phẩm tốt từ lô II là C212=66
Gọi A là biến cố: “ cả 4 sản phầm được chọn ra đều là sản phẩm tốt”
⇒n(A)=45.66=2970
Vậy P(A)=2970C215.C215=66245
Câu 3.
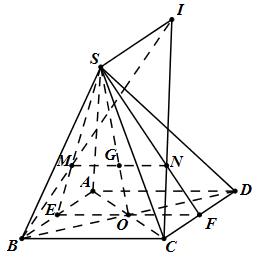
a) Gọi E, F lần lượt là trung điểm của AB và CD.
Trong (SEF) có: SMSE=SNSF=23⇒MN//EF (Định lí Ta-lét đảo)
Mà EF⊂(ABCD)⇒MN//(ABCD).
b) Xét 2 mặt phẳng (SAB) và (SBC) có:
S chung;
AB // CD (ABCD là hình chữ nhật)
⇒∃Δ thỏa mãn
{S∈Δ(1)AB//CD//Δ(2)
BM⊂(SAB);CM⊂(SCD)⇒I=BM∩CN nằm trên giao tuyến của (SAB) và (SCD).
⇒I∈Δ (3)
Từ (1), (2) và (3) ⇒SI//AB//CD⇒SI//CD⇒SI//FC
Áp dụng định lí Ta-lét ta có: SIFC=SNNF
Nên N là trọng tâm tam giác SCD ⇒SNNF=2⇒SIFC=2
SIFC=SICD2=2SICD=2⇔SICD=1
c) Ta xác định G là giao điểm của MN và (SAC), MN⊂(SEF)
EF là đường nối 2 trung điểm của hình chữ nhật ABCD, gọi AC∩BD=O
⇒EF đi qua O và AC∩EF=O.
Xét (SAC) và (SEF) có:
S chung ;
AC∩E=O
⇒(SAC)∩(SEF)=SO
G=SO∩MN=MN∩(SAC)(4)
Ta lại có:
MN // EF
G∈MN;O∈EF
S, G, O thẳng hàng
⇒GM//EO
Áp dụng định lí Ta-lét ta có : SMSE=SGSO=23(5)
SO là trung tuyến của tam giác SBD (6)
Từ (4), (5) và (6) ta có G là trọng tâm tam giác SBD.
Câu 4:
*) Ta sẽ cần tính xác suất để bạn A làm được :
+) Đúng k câu trên 50 câu.
+) Sai (50 - k) câu còn lại.
*) A làm đúng k câu, số cách chọn k câu trong 50 câu là Ck50
Xác suất đúng 1 câu là 14 xác suất sai 1 câu là 34
⇒ Xác suất đún k câu là (14)k xác suất sai (50 - k) câu là (34)50−k
Vậy xác suất để bạn A đúng k câu là: Pk=Ck50(14)k(34)50−k
Xét:
Pk+1Pk=Ck+150(14)k+1(34)50−(k+1)Ck50(14)k(34)50−k=50!(k+1)!(50−k−1)!.1450!k!(50−k)!.34=50!(k+1)!(50−k−1)!.14.k!(50−k)!50!.43=50−k3(k+1)
Ta có:
Pk+1Pk>1⇔50−k3(k+1)>1⇔50−k>3k+3⇔k<474=11,75⇒k∈{1;2;...;11}Pk+1Pk<1⇔50−k3(k+1)<1⇔50−k<3k+3⇔k>474=11,75⇒k∈{12;13;...;49}k=1⇒P2>P1k=2⇒P3>P2....k=11⇒P12>P11k=12⇒P13<P12...k=49⇒P50<P49⇒P11>P10>...>P1P12>P13<...>P50
Vì xác suất làm đúng câu k của học sinh A đạt giá trị lớn nhất nên [k=11k=12
Ta có P12P11>1
⇒P12>P11⇒k=12 thỏa mãn
Vậy khi đó A làm đúng 12 câu và sai 38 câu, số điểm của A là 12.0,2=2,4 điểm.
Xem lời giải chi tiết đề thi học kì 1 tại Tuyensinh247.com

