Đề bài
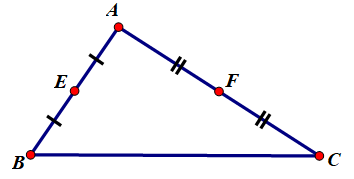
Cho tam giác \(ABC.\) Gọi \(E\) và \(F\) tương ứng là trung điểm của \(AB\) và \(AC.\) Tìm một phép vị tự biến \(B\) và \(C\) tương ứng thành \(E\) và \(F.\)
Video hướng dẫn giải
Lời giải chi tiết
Theo đề bài ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
AE = \frac{1}{2}AB\\
AF = \frac{1}{2}AC
\end{array} \right.\quad \Rightarrow \;\left\{ \begin{array}{l}
\overrightarrow {AE} = \frac{1}{2}\overrightarrow {AB} \\
\overrightarrow {AF} = \frac{1}{2}\overrightarrow {AC}
\end{array} \right.\quad \\
\Rightarrow \;\;\left\{ \begin{array}{l}
{V_{\left( {A,\frac{1}{2}} \right)}}(B) = E\\
{V_{\left( {A,\frac{1}{2}} \right)}}(C) = F
\end{array} \right.
\end{array}\)
Vậy: Phép vị tự tâm \(A\), tỉ số \(1 \over 2\) biến điểm \(B\) thành điểm \(E\) và biến điểm \(C\) thành điểm \(F.\)