Đề bài
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi G và H tương ứng là trọng tâm và trực tâm của tam giác, các điểm A′,B′,C′ lần lượt là trung điểm của các cạnh BC,CA,AB.
a) Tìm phép vị tự F biến A,B,C tương ứng thành A′,B′,C′
b) Chứng minh rằng O,G,H thẳng hàng.
c) Tìm ảnh của O qua phép vị tự F
d) Gọi A”,B”,C” lần lượt là trung điểm của các đoạn thẳng AH,BH,CH; A1,B1,C1 theo thứ tự là giao điểm thứ hai của các tia AH,BH,CH với đường tròn (O); A′1,B′1,C′1 tương ứng là chân các đường cao đi qua A,B,C. Tìm ảnh của A,B,C, A1,B1,C1 qua phép vị tự tâm H tỉ số 12
e) Chứng minh chín điểm A′,B′,C′,A”,B”,C”,A′1,B′1,C′1cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác ABC)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Dựa vào định nghĩa phép vị tự và tính chất trọng tâm của tam giác.
b) Chứng minh hai vectơ →GO;→GH cùng phương.
c) Dựa vào định nghĩa phép vị tự.
d) Sử dụng tính chất của phép vị tự: Ảnh của đường tròn qua phép vị tự là 1 đường tròn.
Lời giải chi tiết
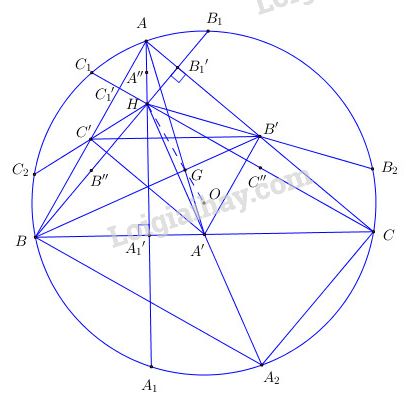
a) Ta có
→GA′=−12→GA;→GB′=−12→GB;→GC′=−12→GC.
Vậy phép vị tự tâm G tỉ số k=−12 biến A,B,C thành A′,B′,C′.
b) A′ là trung điểm của dây BC nên OA′⊥BC
Ta lại có BC//C′B′⇒OA′⊥B′C′. Tương tự B′O⊥A′C′
⇒ Trong tam giác A′B′C′, A′O⊥B′C′,B′O⊥A′C′ nên O là trực tâm của ∆A’B’C’.
H là trực tâm của ∆ABC và O là trực tâm của ∆A’B’C’ nên O là ảnh của H trong phép vị tự tâm G, tỉ số k = - {1 \over 2} \Rightarrow \overrightarrow {GO} = - {1 \over 2}\overrightarrow {GH}
⇒ Ba điểm O, G, H thẳng hàng.
c) Gọi {V_{\left( {G; - {1 \over 2}} \right)}(O)=O'} ta có:
\eqalign{ & \overrightarrow {GO'} = - {1 \over 2}\overrightarrow {GO} \cr & \overrightarrow {GO} = - {1 \over 2}\overrightarrow {GH} \Rightarrow \overrightarrow {OG} = {1 \over 2}\overrightarrow {GH} \cr & \overrightarrow {OG} + \overrightarrow {GO'} = {1 \over 2}\overrightarrow {GH} - {1 \over 2}\overrightarrow {GO} \cr & \Rightarrow \overrightarrow {OO'} = {1 \over 2}\left( {\overrightarrow {GH} - \overrightarrow {GO} } \right) \cr & \Rightarrow \overrightarrow {OO'} = {1 \over 2}\overrightarrow {OH} \cr}
Suy ra O’ là trung điểm của đoạn thẳng OH.
d) Gọi A'', B'', C'' lần lượt là trung điểm của AH, BH, CH ta có:
\eqalign{ & \overrightarrow {HA''} = {1 \over 2}\overrightarrow {HA} \cr & \overrightarrow {HB''} = {1 \over 2}\overrightarrow {HB} \cr & \overrightarrow {HC''} = {1 \over 2}\overrightarrow {HC} \cr}
Vậy A”, B”, C” là ảnh của các điểm A, B, C trong phép vị tự {V_{\left( {H;{1 \over 2}} \right)}}.
Ta dễ dàng chứng minh được A_1',B_1',C_1' theo thứ tự là trung điểm của các đoạn thẳng H{A_1},H{B_1},H{C_1} nên:
\eqalign{ & \overrightarrow {H{A_1}'} = {1 \over 2}\overrightarrow {H{A_1}} \cr & \overrightarrow {H{B_1}'} = {1 \over 2}\overrightarrow {H{B_1}} \cr & \overrightarrow {H{C_1}'} = {1 \over 2}\overrightarrow {H{C_1}} \cr}
Như vậy A_1',B_1',C_1' theo thứ tự là ảnh của các điểm A_1, B_1, C_1 trong phép vị tự {V_{\left( {H;{1 \over 2}} \right)}}
e) Gọi A_2, B_2, C_2 theo thứ tự là các điểm xuyên tâm đối của các điểm A, B, C qua tâm O của đường tròn. Ta dễ dàng chứng minh được tứ giác BHCA_2 là hình bình hành, do đó H và A_2 đối xứng qua A’, ta có:
\eqalign{ & \overrightarrow {HA'} = {1 \over 2}\overrightarrow {H{A_2}} \cr & \overrightarrow {HB'} = {1 \over 2}\overrightarrow {H{B_2}} \cr & \overrightarrow {HC'} = {1 \over 2}\overrightarrow {H{C_2}} \cr}
Như vậy, các điểm A’, B’, C’ theo thứ tự là ảnh của các điểm A_2, B_2, C_2 trong phép vị tự {V_{\left( {H;{1 \over 2}} \right)}}.
Từ đó ta có:
Chín điểm A’, B’,C’,A”, B”,C”, A_1',B_1',C_1' theo thứ tự là ảnh của các điểm A,B,C,{A_1},{B_1},{C_1},{A_2},{B_2},{C_2} trong phép tự vị {V_{\left( {H;{1 \over 2}} \right)}} mà chín điểm A,B,C,{A_1},{B_1},{C_1},{A_2},{B_2},{C_2} nằm trên đường tròn (O) nên chín điểm A,B,C,{A_1},{B_1},{C_1},{A_2},{B_2},{C_2} nằm trên đường tròn ảnh của đường tròn (O) trong phép vị tự {V_{\left( {H;{1 \over 2}} \right)}}

