Câu hỏi 1:
Tìm đạo hàm của hàm số y=2cosx
- y′=2sinx
- y′=−sinx
- y′=sinx
- y′=−2sinx
Đáp án:
y′=−2sinx
Phương pháp giải:
(cosx)′=−sinx
Lời giải chi tiết:
(2cosx)′=2.(cosx)′=−2sinx
Câu hỏi 2:
Tìm đạo hàm của hàm số y=tanx với x≠π2+kπ,k∈Z.
- y′=1sin2x.
- y′=1sin2x.
- y′=−1cos2x.
- y′=1cos2x.
Đáp án:
y′=1cos2x.
Phương pháp giải:
Đạo hàm của hàm lượng giác.
Lời giải chi tiết:
y′=1cos2x
Câu hỏi 3:
Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh họa).
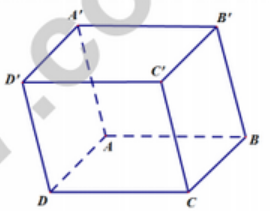
Mệnh đề nào sau đây đúng?
- →AC′=→AD+→AC+→AA′
- →AC′=→AB+→AD+→AA′
- →AC′=→AB+→AC+→AA′.
- →AC′=→AB+→AD+→AC.
Đáp án:
→AC′=→AB+→AD+→AA′
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
ACC’A’ và ABCD là hình bình hành nên: →AC′=→AC+→AA′=→AB+→AD+→AA′
Câu hỏi 4:
Trong không gian, cho đoạn thẳng AB có trung điểm là I, (α) là mặt phẳng trung trực của đoạn thẳng AB. Phát biểu nào sau đây đúng?
- (α) qua I và vuông góc với AB.
- (α) qua A và vuông góc với AB.
- (α) qua I và không vuông góc với AB.
- (α) qua B và vuông góc với AB.
Đáp án:
(α) qua I và vuông góc với AB.
Phương pháp giải:
Định nghĩa mặt phẳng trung trực.
Lời giải chi tiết:
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với AB tại trung điểm của AB.
Câu hỏi 5:
Hàm số nào dưới đây liên tục trên toàn bộ tập số thực R ?
- y=tanx.
- y=x−12x+1.
- y=x2−3x+56.
- y=1x2−2.
Đáp án:
y=x2−3x+56.
Phương pháp giải:
Hàm đa thức luôn liên tục trên R
Lời giải chi tiết:
y=x2−3x+56 là hàm đa thức nên liên tục trên R.
Câu hỏi 6:
Mệnh đề nào sau đây sai?
- (c)′=0 ( c là hằng số).
- (√x)′=1√x(x>0).
- (xn)′=nxn−1(n∈N,n>1).
- (x)′=1.
Đáp án:
(√x)′=1√x(x>0).
Phương pháp giải:
Sử dụng quy tắc đạo hàm các hàm cơ bản.
Lời giải chi tiết:
B sai vì (√x)′=12√x.
Câu hỏi 7:
limx→222x−5x−2 bằng
- −∞
- 52.
- +∞
- 2
Đáp án:
−∞
Phương pháp giải:
limx→x0+f(x)=L<0;limx→x0+g(x)=0 và g(x)>0 khi x→x0+ thì limx→x+0f(x)g(x)=−∞
Lời giải chi tiết:
limx→222x−5=−1<0limx→22(x−2)=0;x−2>0∀x>2
⇒limx→222x−5x−2=−∞
Câu hỏi 8:
Gọi S là tổng của cấp số nhân lùi vô hạn (un) có công bội q(|q|<1). Khẳng định nào sau đây đúng ?
- S=u11−q.
- S=u11+q.
- S=1u1−q.
- S=u1q−1.
Đáp án:
S=u11−q.
Phương pháp giải:
Lý thuyết tổng cấp số nhân lùi vô hạn (un) có công bội q(|q|<1).
Lời giải chi tiết:
S=u1+u2+...=u1(1+q+q2+...)=u11−q
Câu hỏi 9:
Cho hai hàm số u=u(x),v=v(x) có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh đề nào sau đây sai ?
- (u+v)′=u′+v′.
- (u−v)′=u′−v′.
- (ku)′=ku′ ( k là hằng số).
- (uv)′=u′v′.
Đáp án:
(uv)′=u′v′.
Phương pháp giải:
Sử dụng quy tắc đạo hàm của tổng hiệu, tích.
Lời giải chi tiết:
D sai vì (u.v)′=u′.v+v′.u
Câu hỏi 10:
Cho hai hàm số f(x),g(x) thỏa mãn limx→1f(x)=−5 và limx→1g(x)=2. Giá trị của limx→1[f(x)−g(x)] bằng
- 7
- 3
- −7
- −3
Đáp án:
−7
Phương pháp giải:
limx→x0[f(x)−g(x)]=limx→x0f(x)−limx→x0g(x)
Lời giải chi tiết:
limx→1[f(x)−g(x)]=limx→1f(x)−limx→1g(x)=−5−2=−7
Câu hỏi 11:
Cho lăng trụ ABC.A’B’C’(hình vẽ minh họa)
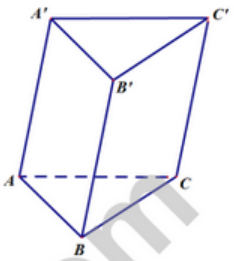
Vecto ¯A′A không phải là vecto chỉ phương của đường thẳng nào sau đây?
- BB’
- AA’
- BC
- CC’
Đáp án:
BC
Phương pháp giải:
→A′A là vecto chỉ phương của mọi đường thẳng song song với A′A
Lời giải chi tiết:
BC không song song với AA′ nên BC không nhận AA′ làm vecto chỉ phương.
Câu hỏi 12:
Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng α. Phát hiểu nào sau đây đúng?
- Nếu a//(α) và b//(α) thì a⊥b.
- Nếu a⊥(α) và b⊥(α) thì a⊥b.
- Nếu b//(α) và a⊥(α) thì a⊥b.
- Nếu b/4(α) và a⊥b thì a⊥(α).
Đáp án:
Nếu b//(α) và a⊥(α) thì a⊥b.
Phương pháp giải:
Lý thuyết đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
Nếu b//(α) và a⊥(α) thì a⊥b.
Câu hỏi 13:
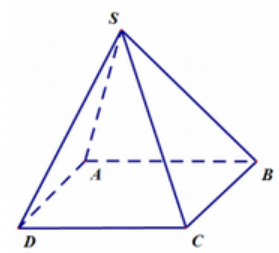
Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh họa)

Hãy chọn khẳng định đúng?
- BD⊥(SAC).
- CD⊥(SAD).
- AC⊥(SBD).
- BC⊥(SAB).
Đáp án:
BD⊥(SAC).
Phương pháp giải:
2 đường chéo của hình thoi vuông góc với nhau.
Lời giải chi tiết:
ABCD là hình thoi nên BD⊥AC.
Mà BD⊥SA và AC và SA cắt nhau tại A nên BD⊥(SAC).
Câu hỏi 14:
limx→2x2−4x−2 bằng
- +∞
- 0
- 2
- 4
Đáp án:
4
Phương pháp giải:
Khử mẫu. Thay x=2 tìm giới hạn.
Lời giải chi tiết:
limx→2x2−4x−2=limx→2(x−2)(x+2)x−2=limx→2(x+2)=4
Câu hỏi 15:
limn+12n−3 bằng
- 0
- −∞.
- 12.
- −13.
Đáp án:
12.
Phương pháp giải:
Chia cả tử và mẫu cho n. Sử dụng lim1n=0
Lời giải chi tiết:
limn+12n−3=limn(1+1n)2(1−3n)=12
Câu hỏi 16:
Cho hình chóp S.ABCD có đáy là hình bình hành (hình vẽ minh họa).

Hãy chọn khẳng định đúng.
- →SA+→SC=→SB+→SD
- →SA+→AB=→SD+→DC
- →SA+→AD=→SB+→BC.
- →SA+→SB=→SC+→SD
Đáp án:
→SA+→SC=→SB+→SD
Phương pháp giải:
M là trung điểm của AB thì →CA+→CB=2→CM.
Lời giải chi tiết:
Gọi O là giao điểm của AC và BD.
Khi đó O là trung điểm chung của AC và BD.
→SC+→SA=2→SO;→SB+→SD=2→SO⇒→SC+→SA=→SB+→SD
Câu hỏi 17:
Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau (hình vẽ minh họa).
Số đo góc giữa hai đường thẳng SA và CD bằng
- 120∘.
- 30∘.
- 60∘.
- 90∘.
Đáp án:
60∘.
Phương pháp giải:
Từ một điểm trên a và kẻ đường thẳng c song song với đường thẳng b thì góc giữa a và b bằng góc giữa c và b.
Lời giải chi tiết:
CD||AB⇒^(SA,CD)=^(SA,AB)=^SAB=60∘
Câu hỏi 18:
Tìm đạo hàm của hàm số y=√x2+1.
- y′=2x√x2+1.
- y′=x√x2+1.
- y′=2x+12√x2+1.
- y′=12√x2+1.
Đáp án:
y′=x√x2+1.
Phương pháp giải:
Sử dụng (√u)′=u′2√u
Lời giải chi tiết:
y′=(x2+1)′2√x2+1=2x2√x2+1=x√x2+1
Câu hỏi 19:
Cho hàm số y=sin2x. Mệnh đề nào sau đây đúng?
- y′(π6)=√3.
- y′(π6)=−1.
- y′(π6)=1.
- y′(π6)=12.
Đáp án:
y′(π6)=1.
Phương pháp giải:
(sinu)′=u′.cosu
Thay x=π6 vào đạo hàm.
Lời giải chi tiết:
y′=(sin2x)′=2.cos2x⇒y′(π6)=2.cosπ3=1
Câu hỏi 20:
Một chất điểm chuyển động theo phương trình S=−13t3+6t2, trong đó t>0,t được tính bằng giây (s) và S tính bằng mét (m). Vận tốc của chất điểm tại thời điểm t=3 (giây) bằng
- 33m/s
- 9m/s.
- 27m/s.
- 3m/s.
Đáp án:
27m/s.
Phương pháp giải:
Hàm số của vận tốc: v(t)=S′(t).
Thay t=3 vào tính v(3).
Lời giải chi tiết:
v(t)=S′(t)=−t2+12t⇒v(3)=−9+36=27m/s
Câu hỏi 21:
lim1−3n2n+4.3n bằng
- 32.
- 0
- −14.
- −1
Đáp án:
−14.
Phương pháp giải:
Chia cả tử và mẫu cho 3n.
lim13n=0;lim2n3n=0
Lời giải chi tiết:
lim1−3n2n+4.3n=lim13n−12n3n+4=−14
Câu hỏi 22:
(2 điểm)
Câu 1:
Cho hàm số f(x)={√x+6−2x+2khix>−2x+2mkhix≤−2. Tìm tất cả các giá trị của tham số m để hàm số f(x) liên tục tại điểm x=−2.
Phương pháp giải:
Lời giải chi tiết:
Câu 2:
Cho hàm số y=f(x)=2x−1x+1, có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng d:y=−3x+4.
Phương pháp giải:
Tìm f′(x).
Tiếp tuyến của hàm số tại x0: y=f′(x0).(x−x0)+f(x0).
Lời giải chi tiết:
f′(x)=3(x+1)2
Tiếp tuyến vuông góc với đường thẳng d:y=−3x+4 nên
3(x+1)2=13⇔|x+1|=3⇔[x=2x=−4
Câu hỏi 23:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, α là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Xác định α và tính sinα.
Phương pháp giải:
Xác định đường thẳng qua G và vuông góc với (SAC).
Góc giữa CG và (SAC) là góc giữa CG và hình chiếu của nó lên (SAC).
Lời giải chi tiết:
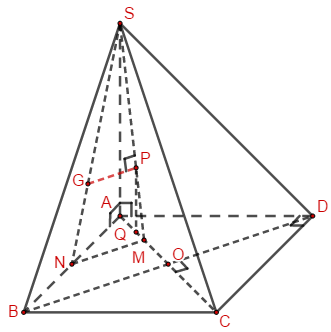
Gọi O là tâm của ABCD.
M là trung điểm của AO, N là trung điểm của AB.
Qua G kẻ GP song song với MN (P∈SM).
Ta có ABCD là hình vuông nên BD⊥AC. Mà MN||BD⇒MN⊥AC.
Ta lại có MN⊥SA(SA⊥(ABCD))
=> MN⊥(SAC)
GP||MN⇒GP⊥(SAC)⇒^(CG,(SAC))=^GCP=α
GP=23MN=23.12OB=13.12BD=16.a√2
Kẻ PQ||SA⇒PQ=13SA=2a3
CQ=13MA+3MA=103.MA=103.14AC=56AC=5.a√26⇒CP=√CQ2+PQ2=√25a218+4a29=a√116⇒CG=√CP2+GP2=a√173⇒sinα=GPCG=√26.3√17=1√34

