Đề bài
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn thẳng SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Áp dụng định lý Pi-ta-go cho tam giác vuông.
b) Chứng minh BD⊥(SAC) và sử dụng lý thuyết: Nếu một đường thẳng vuông góc với một phẳng thì mọi mặt phẳng chứa đường thẳng này đều vuông góc mặt phẳng kia.
c) Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
Lời giải chi tiết
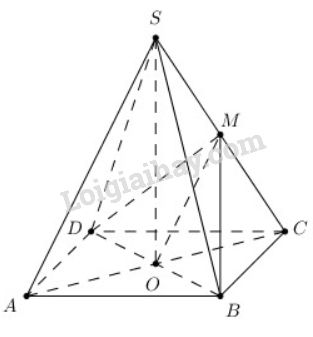
a) Hình chóp tứ giác đều nên SO⊥(ABCD). Do đó SO⊥AC
Tam giác ABD vuông tại A nên BD=√AB2+AD2=a√2 ⇒AO=12BD=a√22
Xét tam giác SOA vuông tại O:
SO=√SA2−AO2=a√22.
b) BD⊥AC , BD⊥SO nên BD⊥(SAC),
Mà BD⊂(MBD) do đó (MBD)⊥(SAC).
c) OM=SC2=a2 (trung tuyến ứng với cạnh huyền của tam giác vuông thì bằng nửa cạnh ấy).
ΔSDC=ΔSBC(c.c.c) suy ra DM=BM suy ra tam giác BDM cân tại M
OM vừa là trung tuyến đồng thời là đường cao nên OM⊥BD
(MBD)∩(ABCD)=BDOM⊥BDOC⊥BD}
⇒ góc giữa hai mặt phẳng (MBD) và (ABCD) là ^MOC
Ta có OM=SC2=a2 hay OM=MC
Tam giác OMC vuông cân tại M nên ^MOC=450.
Vậy góc giữa hai mặt phẳng (MBD) và (ABCD) là 450.

