Video hướng dẫn giải
Trong mặt phẳng tọa độ OxyOxy, cho các điểm A(1;1),B(0;3),C(2;4)A(1;1),B(0;3),C(2;4) .Xác định ảnh của tam giác ABCABC qua các phép biến hình sau.
LG a
Phép tịnh tiến theo vectơ →v=(2;1)→v=(2;1).
Phương pháp giải:
Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải chi tiết:
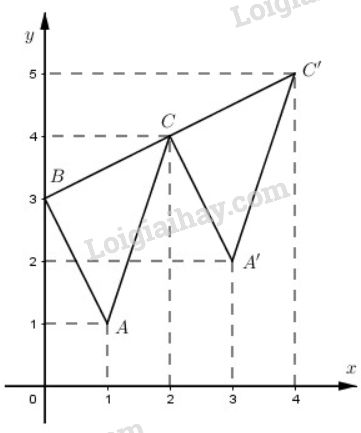
Trong phép tịnh tiến theo vectơ →v=(2;1)→v=(2;1) thì các đỉnh A,B,CA,B,C có ảnh là các điểm tương ứng A′,B′,C′.
Từ biểu thức tọa độ
{x′=2+xy′=1+y
Ta có:
A(1;1)⇒A′(3;2)
B(0;3)⇒B′(2;4)
C(2;4)⇒C′(4;5)
Tam giác A′B′C′, ảnh của tam giác ABC trong phép tịnh tiến theo vectơ →v là tam giác có ba đỉnh A′(3;2),B′(2;4),C′(4;5)
Dễ thấy đỉnh B′ của ∆A′B′C′ trùng với đỉnh C của ∆ABC.
LG b
Phép đối xứng qua trục Ox
Phương pháp giải:
Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải chi tiết:
Qua phép đối xứng trục Ox, biểu thức tọa độ là :
{x′=xy′=−y
Do đó ta có: ∆A′B′C′ có các đỉnh A′(1;−1),B′(0;−3),C′(2;−4)
LG c
Phép đối xứng qua tâm I(2;1).
Phương pháp giải:
Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải chi tiết:
Trong phép đối xứng qua tâm I(2;1), đỉnh A→A′ thì I là trung điểm của AA′. Gọi tọa độ A′ là (x;y) thì:
2=1+x2⇒x=31=1+y2⇒y=1
⇒A′(3;1)
Tương tự, ta có ảnh B′,C′ của các đỉnh B,C là B′(4;−1),C′(2;−2)
LG d
Phép quay tâm O góc 900.
Phương pháp giải:
Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải chi tiết:
Trong phép quay tâm O, góc quay 900 thì tia Ox biến thành tia Oy, tia Oy biến thành tia Ox
Điểm A(1;1)→A′(−1;1)
B(0;3)→B′(−3;0)
C(2;4)→C′(−4;2)
LG e
Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k=−2
Phương pháp giải:
Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải chi tiết:
Trong phép đổi xứng qua Oy. ∆ABC biến thành ∆A1B1C1, ta có:
A(1;1)→A1(−1;1)
B(0;3)→B1(0;3)
C(2;4)→C1(−2;4)
Với phép vị tự tâm O tỉ số k=−2 thì ∆A1B1C1→∆A′B′C′
A1(−1;1)→A′(2;−2)
B1(0;3)→B′(0;−6)
C1(−2;4)→C′(4;−8)
Vậy trong phép đồng dạng đã cho thì ∆ABC có ảnh là ∆A′B′C′ với A′(2;−2),B′(0;−6),C′(4;−8)

