Đề bài
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi H là tâm tam giác đều ABC ⇒SH⊥(ABC)⇒d(S;(ABC))=SH
Áp dụng định lí Pytago trong tam giác vuông để tính SH.
Lời giải chi tiết
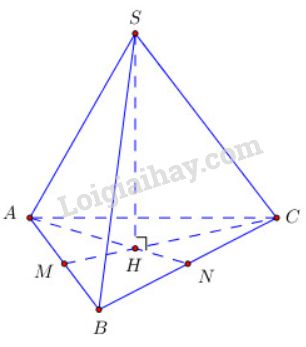
Gọi H là tâm của tam giác đều ABC ta có SH⊥(ABC)
⇒d(S,(ABC))=SH
Gọi N là trung điểm của BC.
⇒BN=NC=3a2
Tam giác ABN vuông tại N nên:
AN=√AB2−BN2 =√(3a)2−(3a2)2=3a√32
H là trọng tâm tam giác ABC ⇒AH=23.AN=a√3
Áp dụng định lí Pytago vào tam giác vuông SAH ta có:
SH=√SA2−AH2=√4a2−(a√3)2=a.
Vậy d(S;(ABC))=SH=a.

