Đề bài
A. PHẦN TRẮC NGHIỆM (3 điểm):
Câu 1. lim(2n+3) bằng
A. +∞. B. 3.
C. 5. D. −∞.
Câu 2. Biết lim1+3n3n+1=ab ( a, b là hai số tự nhiên và ab tối giản). Giá trị của a+b bằng
A. 3. B. 13.
C. 0. D. 4.
Câu 3. limx→1(x2−2x−3) bằng
A. −5. B. 0.
C. 4. D. −4.
Câu 4. Biết limx→−∞x+21−2x=−ab ( a, b là hai số tự nhiên và ab tối giản). Giá trị của a−b bằng
A. 3. B. −1.
C. −3. D. 1.
Câu 5: lim2n+3n2+2n+4 bằng
A. 2. B. 1.
C. 0. D. +∞.
Câu 6. Biết rằng phương trình x5+x3+3x−1=0 có ít nhất 1 nghiệm x0, mệnh đề nào dưới đây đúng ?
A. x0∈(0;1).
B. x0∈(−1;0).
C. x0∈(1;2).
D. x0∈(−2;−1).
Câu 7. Cho hàm số y=x3−2x2+3x+2. Giá trị của y′(1) bằng
A. 7. B. 4.
C. 2. D. 0.
Câu 8. Đạo hàm của hàm số y=sin2x bằng
A. y′=cos2x.
B. y′=2cos2x.
C. y′=−2cos2x.
D. y′=−cos2x.
Câu 9. Đạo hàm của hàm số y=x+1x−1 bằng
A. y′=−2(x−1)2.
B. y′=1.
C. y′=2(x−1)2.
D. y′=−2x−1.
Câu 10. Đạo hàm của hàm số y=√x2+1 bằng
A. y′=√2x.
B. y′=x2√x2+1.
C. y′=12√x2+1.
D. y′=x√x2+1.
Câu 11. Biết AB cắt mặt phẳng (α) tại điểm I thỏa mãn IA=3IB, mệnh đề nào dưới đây đúng ?
A. 4d(A,(α))=3d(B,(α)).
B. 3d(A,(α))=d(B,(α)).
C. 3d(A,(α))=4d(B,(α)).
D. d(A,(α))=3d(B,(α)).
Câu 12. Mệnh đề nào dưới đây sai ?
A. Đường thẳng vuông góc với mặt phẳng khi và chỉ khi góc giữa chúng bằng 90o.
B. Góc giữa hai đường thẳng bằng góc giữa 2 vectơ chỉ phương của 2 đường thẳng đó.
C. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng 90o.
D. Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1 (1 điểm). Tính các giới hạn sau:
a.limx→−∞(x3−2x2+x+1);
b. limx→3√x+1−2x−3.
Câu 2 (1 điểm). Tính đạo hàm cấp 1 của mỗi hàm số sau:
a. y=(x+2√x)(x2+4);
b. y=cot22x+tanx+12.
Câu 3 (1 điểm). Tìm giá trị của tham số a để hàm số f(x)={x2+4x−5x−1khix≠12x+akhix=1 liên tục tại x0=1.
Câu 4 (1 điểm). Cho hàm sốf(x)=cos2x. Gọi (C) là đồ thị của hàm số y=f(50)(x). Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x=π6.
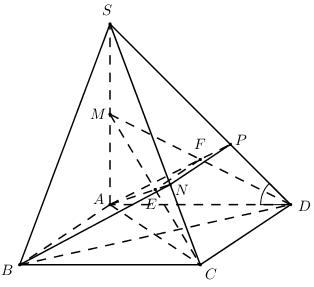
Câu 5 (3 điểm). Cho hình chópS.ABCD có đáy ABCD là hình vuông cạnha, SA⊥(ABCD) và góc giữa SDvới mặt đáy bằng 45o. Gọi M,N,P lần lượt là các điểm trên cạnh SA,SC,SD sao cho SM=MA,SN=2NC và SP=2PD.
a. Chứng minh rằng (SAC)⊥BD;(SAB)⊥(SBC).
b. Chứng minh rằng AP⊥NP.
c. Tính côsin của góc giữa 2 mặt phẳng (MCD) và (BNP).
Lời giải chi tiết
A. PHẦN TRẮC NGHIỆM:
| 1. A | 2. D | 3. D | 4. B | 5. C | 6. A |
| 7. C | 8. B | 9. A | 10. D | 11. D | 12. B |
Câu 1:
Cách giải:
lim(2n+3)=+∞
Chọn A.
Câu 2:
Phương pháp:
Chia cả tử và mẫu cho 3n+1.
Cách giải:
lim1+3n3n+1=lim13n+1+131=13⇒{a=1b=3⇒a+b=1+3=4
Chọn D.
Câu 3:
Phương pháp:
Hàm số y=f(x) liên tục tại x=x0⇔limx→x0f(x)=f(x0).
Cách giải:
limx→1(x2−2x−3)=12−2.1−3=−4
Chọn D.
Câu 4:
Phương pháp:
Chia cả tử và mẫu cho x.
Cách giải:
limx→−∞x+21−2x=limx→−∞1+2x1x−2=−12⇒{a=1b=2⇒a−b=−1.
Chọn B.
Câu 5:
Phương pháp:
Chia cả tử và mẫu cho n2.
Cách giải:
lim2n+3n2+2n+4=lim2n+3n21+2n+4n2=0
Chọn C.
Câu 6:
Phương pháp:
Hàm số y=f(x) liên tục trên (a;b) và có f(a).f(b)<0⇒ Phương trình f(x)=0 có ít nhất 1 nghiệm x0∈(a;b).
Cách giải:
Hàm số y=x5+x3+3x−1 liên tục trên R nên hàm số liên tục trên (0;1).
Ta có: {f(0)=−1f(1)=4⇒f(0).f(−1)<0
⇒ Tồn tại ít nhất 1 nghiệm x0∈(0;1).
Chọn A.
Câu 7:
Phương pháp:
Sử dụng công thức (xn)′=nxn−1(n≠−1).
Cách giải:
y′=3x2−4x+3
⇒y′(1)=3.12−4.1+3=2.
Chọn C.
Câu 8:
Phương pháp:
Sử dụng công thức (sinkx)′=kcoskx.
Cách giải:
y′=(sin2x)′=2cos2x.
Chọn B.
Câu 9:
Phương pháp:
Sử dụng quy tắc (uv)′=u′v−uv′v2.
Cách giải:
Ta có: y′=x−1−(x+1)(x−1)2=−2(x−1)2.
Chọn A.
Chú ý: Có thể sử dụng công thức tính nhanh (ax+bcx+d)′=ad−bc(cx+d)2.
Câu 10:
Phương pháp:
Sử dụng công thức (√u)′=u′2√u.
Cách giải:
y′=(√x2+1)′=(x2+1)′2√x2+1=2x2√x2+1=x√x2+1
Chọn D.
Chú ý: Chú ý khi tính đạo hàm của hàm hợp.
Câu 11:
Phương pháp:
Cho (P) và A,B∉(P). Gọi M=AB∩(P) ta có: d(A;(P))d(B;(P))=AMBM.
Cách giải:
Ta có: AB∩(α)=I và AIBI=3
⇒d(A;(α))d(B;(α))=AIBI=3⇒d(A;(α))=3d(B;(α))
Chọn D.
Câu 12:
Phương pháp:
Góc giữa hai đường thẳng luôn là góc nhọn.
Cách giải:
Góc giữa hai đường thẳng bằng góc giữa 2 vectơ chỉ phương của 2 đường thẳng đó là mệnh đề sai.
Chọn B.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1:
Phương pháp:
a) Đặt x3 ra ngoài và xét dấu.
b) Nhân cả tử và mẫu với biểu thức liên hợp của mẫu để khử dạng 00.
Cách giải:
a) limx→−∞(x3−2x2+x+1)
=limx→−∞x3(1−2x+1x2+1x3) =−∞
Vì limx→−∞x3=−∞ và limx→−∞(1−2x+1x2+1x3)=1>0
b) limx→3√x+1−2x−3
=limx→3(√x+1−2)(√x+1+2)(x−3)(√x+1+2)=limx→3x+1−4(x−3)(√x+1+2)=limx→3x−3(x−3)(√x+1+2)=limx→31√x+1+2=14
Câu 2:
Phương pháp:
a) Sử dụng quy tắc (uv)′=u′v+uv′.
b) Sử dụng các công thức tính đạo hàm hàm lượng giác.
Cách giải:
a)
y=(x+2√x)(x2+4)⇒y′=(x+2√x)′(x2+4)+(x+2√x)(x2+4)′=(1+1√x)(x2+4)+2x(x+2√x)=3x2+5x√x+4√x+4.
b)
y=cot22x+tanx+12⇒y′=2.cot2x(cot2x)′+(x+12)′cos2x+12=2.cot2x−(2x)′sin22x+12cos2x+12=4cot2x.1x2sin22x+12cos2x+12.
Câu 3:
Phương pháp:
Hàm số y=f(x) liên tục tại x=x0⇔limx→x0f(x)=f(x0)
Cách giải:
Ta có:
limx→1f(x)=limx→1x2+4x−5x−1=limx→1(x−1)(x+5)x−1=limx→1(x+5)=6f(1)=2+a
Để hàm số liên tục tại x0=1 thì limx→1f(x)=f(1)⇔2+a=6⇔a=4
Câu 4:
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=x0 là y=f′(x0)(x−x0)+f(x0).
Cách giải:
Ta có:
f′(x)=−2sin2xf″
Nên:
\begin{array}{l}{f^{\left( {4k} \right)}} = {2^{4k}}c{\rm{os}}2x\\{f^{\left( {4k + 1} \right)}} = - {2^{4k + 1}}\sin 2x\\{f^{\left( {4k + 2} \right)}} = - {2^{4k + 2}}c{\rm{os}}2x\\{f^{\left( {4k + 3} \right)}} = {2^{4k + 3}}\sin 2x\end{array}.
Do đó (C) là đồ thị hàm số y = {f^{\left( {50} \right)}}\left( x \right) = {f^{\left( {4.12 + 2} \right)}} = - {2^{50}}{\rm{cos}}2x.
Ta có: y' = {f^{\left( {51} \right)}}\left( x \right) = {2^{51}}\sin 2x.
Tiếp tuyến tại điểm x = \frac{\pi }{6} có phương trình:
\begin{array}{l}y = y'\left( {\frac{\pi }{6}} \right)\left( {x - \frac{\pi }{6}} \right) + y\left( {\frac{\pi }{6}} \right)\\ \Leftrightarrow y = {2^{51}}\sin \frac{\pi }{3}\left( {x - \frac{\pi }{6}} \right) - {2^{50}}c{\rm{os}}\frac{\pi }{3}\\y = {2^{51}}\frac{{\sqrt 3 }}{2}\left( {x - \frac{\pi }{6}} \right) - {2^{50}}.\frac{1}{2}\\ \Leftrightarrow y = {2^{50}}\sqrt 3 \left( {x - \frac{\pi }{6}} \right) - {2^{49}}\\ \Leftrightarrow y = {2^{50}}.\sqrt 3 x - \frac{{{2^{50}}\sqrt 3 \pi }}{6} - {2^{49}}\end{array}
Câu 5:
Phương pháp:
a) \left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right).
\left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right).
b) Chứng minh NP vuông góc với mặt phẳng chứa AP.
c) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến.
Cách giải:
a) Ta có:
\begin{array}{l}\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot (SAC)\\\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right).\end{array}
b) Ta có:
\begin{array}{l}\frac{{SN}}{{NC}} = \frac{{SP}}{{PD}} = 2 \Rightarrow NP//CD\,\,\left( 1 \right)\\\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right)\\ \Rightarrow CD \bot AP\,\,\,\left( 2 \right)\end{array}
Từ (1) và (2) suy ra AP \bot NP.
c) Ta có: \left( {BNP} \right) \equiv \left( {ABNP} \right).
Trong \left( {SAC} \right) gọi E = MC \cap AN. Trong \left( {SAD} \right) gọi F = MD \cap AP.
\Rightarrow \left( {ABNP} \right) \cap \left( {MCD} \right) = EF.
\begin{array}{l}\left\{ \begin{array}{l}\left( {ABNP} \right) \supset AB\\\left( {MCD} \right) \supset CD\\AB//CD\\\left( {ABNP} \right) \cap \left( {MCD} \right) = EF\end{array} \right.\\ \Rightarrow EF//AB//CD\end{array}
Mà CD \bot \left( {SAD} \right) \Rightarrow EF \bot \left( {SAD} \right).
\Rightarrow \left\{ \begin{array}{l}EF \bot AF\\EF \bot DF\end{array} \right. \Rightarrow \angle \left( {\left( {ABNP} \right);\left( {MCD} \right)} \right) = \angle \left( {AF;DF} \right)
Ta có \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;AD} \right) = \angle SDA = {40^0}
\Rightarrow \Delta SAD vuông cân tại A.
\Rightarrow SA = AD = a,\,\,SD = a\sqrt 2 \Rightarrow AM = \frac{a}{2} \Rightarrow DM = \frac{{a\sqrt 5 }}{2}.
Áp dụng định lí cosin trong tam giác APD ta có:
\cos {45^0} = \frac{{{a^2} + {{\left( {\frac{{a\sqrt 2 }}{3}} \right)}^2} - A{P^2}}}{{2.a.\frac{{a\sqrt 2 }}{3}}} \Leftrightarrow A{P^2} = \frac{{5{a^2}}}{9} \Rightarrow AP = \frac{{a\sqrt 5 }}{3}
Áp dụng định lí Menelaus trong tam giác SMD ta có :
\begin{array}{l}\frac{{AM}}{{AS}}.\frac{{PS}}{{PD}}.\frac{{FD}}{{FM}} = 1\\ \Leftrightarrow \frac{1}{2}.2.\frac{{FD}}{{FM}} = 1\\ \Leftrightarrow FD = FM\\ \Rightarrow FD = \frac{1}{2}MD = \frac{{a\sqrt 5 }}{4}\end{array}
Áp dụng định lí Menelaus trong tam giác SAP ta có : \frac{{MA}}{{MS}}.\frac{{DS}}{{DP}}.\frac{{FP}}{{FA}} = 1
\Leftrightarrow 1.3.\frac{{FP}}{{FA}} = 1 \Leftrightarrow \frac{{FP}}{{FA}} = \frac{1}{3}
\Rightarrow AF = \frac{3}{4}AP = \frac{{a\sqrt 5 }}{4}.
Áp dụng định lí cosin trong tam giác AFD ta có:
\cos \angle AFD = \frac{{A{F^2} + D{F^2} - A{D^2}}}{{2AF.DF}}
= \frac{{\frac{{5{a^2}}}{{16}} + \frac{{5{a^2}}}{{16}} - {a^2}}}{{2.\frac{{5{a^2}}}{{16}}}} = - \frac{3}{5}
Vậy \cos \angle \left( {\left( {MCD} \right);\left( {BNP} \right)} \right) = \frac{3}{5}.

