Đề bài
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) →AB và →EG;
b) →AF và →EG;
c) →AB và →DH.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa góc giữa hai vector trong không gian.
Lời giải chi tiết
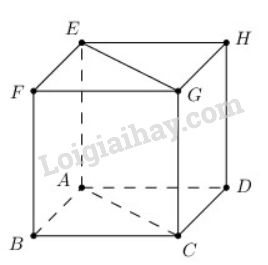
a) (→AB,→EG) =(→AB,→AC)
Vì ABCD là hình vuông nên BAC=450
Vậy (→AB,→AC)=450 hay (→AB,→EG)=450
b) (→AF,→EG)=(→AF,→AC)
=^FAC
Tam giác AFC có các cạnh đều là đường chéo của các hình vuông có độ dài cạnh bằng nhau.
Do đó AF=AC=CF hay tam giác AFC đều.
Suy ra ^FAC=600 hay (→AF,→EG)=600.
c) (→AB,→DH)=(→AB,→AE) =^BAE=900

