Đề bài
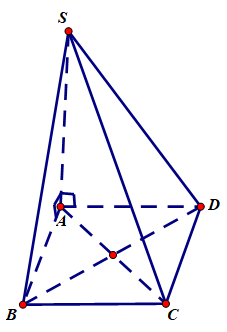
Cho hình vuông \(ABCD\). Dựng đoạn \(AS\) vuông góc với mặt phẳng chứa hình vuông \(ABCD.\)
a) Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng \(SB, SC, SD\) và vuông góc với mặt phẳng \((ABCD)\)
b) Chứng minh rằng mặt phẳng \((SAC)\) vuông góc với mặt phẳng \((SBD)\)
Video hướng dẫn giải
Lời giải chi tiết
a)
\(\begin{array}{l}
SA \bot (ABCD),SA \subset (SAB)\\
\Rightarrow {\rm{ }}\left( {SAB} \right) \bot \left( {ABCD} \right)\\
SA \bot (ABCD),SA \subset (SAD)\\
\Rightarrow {\rm{ }}\left( {SAD} \right) \bot \left( {ABCD} \right)\\
SA \bot (ABCD),SA \subset (SAC)\\
\Rightarrow {\rm{ }}\left( {SAC} \right) \bot \left( {ABCD} \right)
\end{array}\)
b) \(ABCD\) là hình vuông nên \(BD \bot AC\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)
Ta có:
\(\left\{ \begin{array}{l}
BD \bot AC\\
BD \bot SA
\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)
Mà \(BD \subset (SBD)\) nên \((SAC) ⊥ (SBD)\)