Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một tứ giác lồi. Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Xác định thiết diện của hình chóp cắt bởi mặt phẳng \((α)\) đi qua \(O\), song song với \(AB\) và \(SC\). Thiết diện đó là hình gì?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng nội dung của định lí 2:
Cho đường thẳng \(a\) song song với mặt phẳng \(\alpha\). Nếu mặt phẳng \(\beta\) chứa \(a\) và cắt \(\alpha\) theo giao tuyến \(b\) thì \(b\) song song với \(a.\)
Lời giải chi tiết
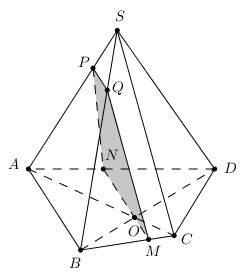
+) \((α) // AB, AB ⊂ (ABCD)\), \(O\) là điểm chung của \((α)\) và \((ABCD)\)
\(\Rightarrow\) Giao tuyến của hai mặt phẳng \(( α)\) và \((ABCD)\) là đường thẳng qua \(O\) và song song với \(AB\).
Trong \((ABCD)\) qua \(O\) kẻ \(MN // AB\) \((M \in BC, N \in AD)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {ABCD} \right) = MN\)
+) \((α) // SC, SC ⊂ (SBC)\), \(M\) là điểm chung của \((α)\) và \((SBC)\)
\(\Rightarrow\) Giao tuyến của hai mặt phẳng \(( α)\) và \((SBC)\) là đường thẳng qua \(M\) và song song với \(SC\).
Trong \((SBC)\) qua \(M\) kẻ \(MQ // SC\) \((Q \in SB)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SBC} \right) = MQ\)
+) \((α) // AB, AB ⊂ (SAB)\), \(Q\) là điểm chung của \((α)\) và \((SAB)\)
\(\Rightarrow\) Giao tuyến của hai mặt phẳng \(( α)\) và \((SAB)\) là đường thẳng qua \(Q\) và song song với \(AB\).
Trong \((SAB)\) qua \(Q\) kẻ \(QP // AB\) \((P \in SA)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = QP\)
+) \( \Rightarrow \left( \alpha \right) \cap \left( {SAD} \right) = NP\)
Vậy thiết diện của hình chóp khi cắt bởi mặt phẳng \((\alpha)\) là tứ giác \(MNPQ\) có \(MN//PQ//AB\)
Vậy thiết diện là hình thang \(MNPQ\).

