Đề bài
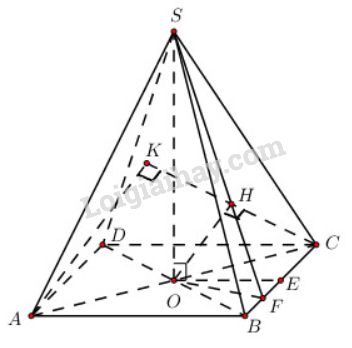
Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc ^BAD=600. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO=3a4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC)
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh BC⊥(SOF).
b) Dựng và tính khoảng cách từ O đến mặt phẳng (SBC). Chứng minh d(A;(SBC))=2d(O;(SBC)).
Lời giải chi tiết
a) Theo giả thiết ^BAD=600 nên theo tính chất của hình thoi ^BCD=600 hay tam giác BDC đều.
⇒BD=a⇒BO=12BD=a2; BE=12BC=a2
Xét tam giác BOE có BO=BE=a2 và ^OBE=600 nên tam giác BOE đều
Do đó OF là đường cao và ta được OF⊥BC.
{SO⊥(ABCD)⇒BC⊥SOBC⊥OF ⇒BC⊥(SOF)
Mà BC⊂(SBC)⇒(SOF)⊥(SBC)
b) Kẻ OH⊥SF
{(SOF)⊥(SBC)(SOF)∩(SBC)=SFOH⊥SFOH⊂(SOF)⇒OH⊥(SBC)⇒d(O,(SBC))=OH
Ta có:
Tam giác OBF vuông tại F nên OF=√OB2−BF2 =√(a2)2−(a4)2=a√34
Tam giác SOF vuông tại O có SO=3a4;OF=a√34⇒SF=√SO2+OF2=a√32OH.SF=SO.OF⇒OH=SO.OFSF=3a8
Gọi K là hình chiếu của A trên (SBC), ta có AK//OH
Trong ΔAKC thì OH là đường trung bình, do đó: AK=2OH⇒AK=3a4.
Vậy d(A;(SBC))=3a4

