Đề bài
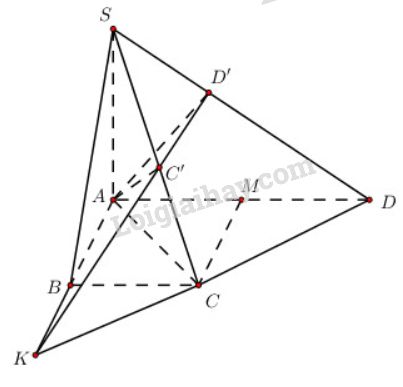
Cho hình thang ABCDABCD vuông tại AA và BB, có AD=2a,AB=BC=aAD=2a,AB=BC=a. Trên tia AxAx vuông góc với mặt phẳng (ABCD)(ABCD) lấy một điểm SS. Gọi C′,D′ lần lượt là hình chiếu vuông góc của A trên SC và SD . Chứng minh rằng :
a) ^SBC=^SCD=900
b) AD′,AC′ và AB cùng nằm trên một mặt phẳng.
c) Chứng minh rằng đường thẳng C′D′ luôn luôn đi qua một điểm cố định khi S di động trên tia Ax.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh BC⊥(SAB);CD⊥(SCD).
b) Chứng minh cả ba đường thẳng AB;AC′;AD′ cùng vuông góc với SD, từ đó kết luận chúng cùng thuộc mặt phẳng đi qua A và vuông góc với SD.
c) Chứng minh ba đường thẳng CD, AB, C'D' đồng quy dựa vào tính chất: Giao tuyến của ba mặt phẳng phân biệt thì đồng quy hoặc đôi một song song.
Lời giải chi tiết
a) Ta có: SA⊥(ABCD)⇒SA⊥BC
SA⊥BCAB⊥BC}⇒SB⊥BC (định lí 3 đường vuông góc) ⇒^SBC=900
⇒ΔSBC vuông tại B.
Gọi M là trung điểm của AD.
Tứ giác ABCM có AB//=CM nên là hình bình hành.
Lại có ˆA=900,AB=CB nên ABCM là hình vuông
⇒CM=a⇒CM=12AD
Tam giác ACD có trung tuyến CM bằng 12 cạnh tương ứng nên nó là tam giác vuông, hay tam giác ACD vuông tại C có AC⊥CD
SA⊥(ABCD)⇒SA⊥CD
SA⊥CDAC⊥CD}⇒SC⊥CD (định lí 3 đường vuông góc)
⇒^SCD=900
⇒ΔSCD vuông tại C.
b) Ta có :
AB⊥SAAB⊥AD}⇒AB⊥(SAD)SD⊂(SAD)}⇒AB⊥SD(1)
CD⊥ACCD⊥SC}⇒CD⊥(SAC)AC′⊂(SAC)}⇒AC′⊥CD
Kết hợp với AC′⊥SC suy ra AC′⊥(SCD)
AC′⊥(SCD)SD⊂(SCD)}⇒AC′⊥SD(2)
Giả thiết cho AD′⊥SD (3)
Từ (1), (2), (3) ta thấy ba đường thẳng AB,AD′,AC′ cùng vuông góc với SD và chúng cùng đi qua A.
Vậy chúng cùng nằm trong mặt phẳng (P) đi qua A và vuông góc với SD.
c) Gọi K là giao điểm của C′D′ với AB.
K∈C′D′⇒K∈(SCD)
K∈AB⇒K∈(ABCD)
⇒K là giao điểm của hai mặt phẳng (SCD) và (ABCD)
Mà (SCD)∩(ABCD)=CD⇒K∈CD.
Vậy ba đường thẳng AB,CD,C′D′ đồng quy tại K và AB,CD cố định suy ra K cố định.
Vậy khi S chạy trên Ax thì C′D′ luôn đi qua điểm cố định là giao điểm K của AB và CD.
loigiaihay.com

