Đề bài
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối diện của tứ diện.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Chứng minh khoảng cách giữa hai cạnh đối của tứ diện đều chính là độ dài đoạn thẳng nối hai trung điểm của hai cạnh đối diện.
- Tính toán dựa vào các tính chất tam giác đều.
Lời giải chi tiết
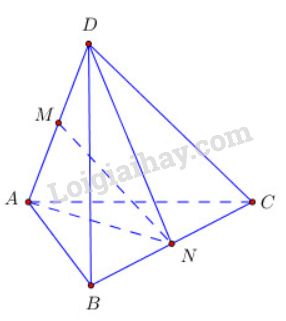
Gọi M,N lần lượt là trung điểm của AD và BC,
Ta có: ΔABC=ΔDBC(c.c.c) ⇒AN=DN (hai đường trung tuyến tương ứng)
⇒ΔAND cân tại N.
⇒ Trung tuyến MN đồng thời là đường cao ⇒MN⊥AD(1)
Chứng minh tương tự, ΔMBC cân tại M⇒MN⊥BC(2)
Từ (1) và (2) suy ra MN là đường vuông góc chung của BC và AD.
⇒d(AD;BC)=MN
Tam giác ABN vuông tại N nên:
AN=√AB2−BN2 =√a2−(a2)2 =a√32
Áp dụng định lí Pytago vào tam giác vuông AMN ta có:
MN=√AN2−AM2=√3a24−a24=a√22
Vậy d(AD;BC)=a√22.

