Đề bài
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, góc ^BAD=600 và SA=SB=SD=a√32
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD)
c) Chứng minh SB vuông góc với BC
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ
Phương pháp giải - Xem chi tiết
a) Gọi H là tâm đường tròn ngoại tiếp tam giác ABD thì SH⊥(ABCD).
Sử dụng định lí Pitago tính SH và SC.
b) Chứng minh mặt phẳng (SAC) chứa 1 đường thẳng vuông góc với mặt phẳng (ABCD).
c) Sử dụng định lí Pitago đảo chứng minh ΔSBC vuông tại B.
d) Sử dụng phương pháp xác định góc giữa hai mặt phẳng.
Lời giải chi tiết
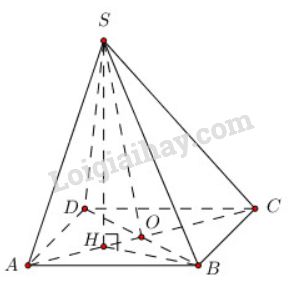
a) Kẻ SH⊥(ABCD)
Do SA=SB=SD suy ra HA=HB=HC
⇒H là tâm đường tròn ngoại tiếp tam giác ABD.
Ta có: AB=AD=a và ^BAD=600 nên ΔABD là tam giác đều cạnh a ⇒AO=a√32,AH=23AO=a√33
Trong tam giác vuông SAH, ta có: SA=a√32;AH=a√33
⇒SH=√SA2−AH2=√3a24−a23=a√156
CH=AC−AH=2AO−AH =2.a√32−a√33=2a√33
Trong tam giác vuông SHC: SC2=SH2+HC2⇒SC=a√72
b) SH⊥(ABCD)SH⊂(SAC)}⇒(SAC)⊥(ABCD)
c) Ta có:
SC2=7a24;BC2=a2;SB2=3a24
⇒SC2=BC2+SB2
⇒ΔSBC vuông tại B ⇒SB⊥BC.
Cách khác:
Ta có: SH⊥(ABD)⇒SH⊥AD.
H là tâm tam giác ABD nên BH⊥AD
{BH⊥ADSH⊥AD⇒AD⊥(SBH)
Mà BC//AD nên BC⊥(SBH)
⇒BC⊥SB
d) Ta có:
DB⊥ACSH⊥(ABCD)⇒SH⊥DB}⇒DB⊥(SAC)⇒{DB⊥OSDB⊥AC
{(SBD)∩(ABCD)=BDSO⊥BD,AC⊥BDSO⊂(SBD)AC⊂(ABCD)
Nên góc giữa (SBD) và (ABCD) bằng góc giữa SO và AC hay ^SOH là góc giữa hai mặt phẳng (SBD) và (ABCD)
Ta có:
SH=a√156 và OH=13AO=13.a√32=a√36
⇒tanφ=SHOH=a√156a√36=√5

