Đề bài
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng.
a) Gọi \(O\) và \(O'\) lần lượt là tâm của các hình bình hành \(ABCD\) và \(ABEF\). Chứng minh rằng đường thằng \(OO'\) song song với các mặt phẳng \((ADF)\) và \((BCE)\).
b) Gọi \(M\) và \(N\) lần lượt là trọng tâm của hai tam giác \(ABD\) và \(ABE\). Chứng minh đường thẳng \(MN\) song song với mặt phẳng \((CEF)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Muốn chứng minh 1 đường thẳng song song với một mặt phẳng ta chứng minh đường thẳng song song với một đường thẳng bất kì trong mặt phẳng.
Lời giải chi tiết
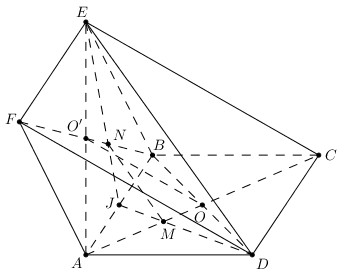
a) Vì \(O\) là tâm của hình bình hành \(ABCD\) nên \(O\) là trung điểm \(AC, BD.\)
\(O'\) là tâm hbh \(ABEF\) nên \(O\) là trung điểm \(AE, BF.\)
Tam giác \(DBF\) có \(OO'\) là đường trung bình nên \(OO' // DF\).
\(DF\) nằm trong mặt phẳng \((ADF)\) nên \(OO' // mp(ADF)\).
\(ΔAEC\) có \(OO’\) là đường trung bình nên \(OO’ // EC,\) mà \(EC ⊂ (BCE)\)
\(⇒ OO’ // (BCE).\)
b) Ta thấy \(mp(CEF)\) chính là \(mp(CEFD).\)
Gọi \(J\) là trung điểm đoạn thẳng \(AB\).
Ta có:
\(M\) là trọng tâm \(ΔABD \Rightarrow \dfrac{{JM}}{{JD}} = \dfrac{1}{3}\)
\(N\) là trọng tâm \(ΔABE \Rightarrow \dfrac{{JN}}{{JE}} = \dfrac{1}{3}\)
\(\Rightarrow \dfrac{{JM}}{{JD}}=\dfrac{{JN}}{{JE}}=\dfrac{1}{3}\Rightarrow MN//ED\)
\(ED\subset (CEFD) \Rightarrow MN//(CEFD)\) hay \(MN//(CEF).\)

