Đề bài
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho →MS = −2→MA và trên đoạn BC lấy điểm N sao cho →NB=−12→NC. Chứng minh rằng ba véctơ →AB, →MN, →SC đồng phẳng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kết quả của định lí 1 về điều kiện để ba vector đồng phẳng.
Trong không gian cho hai vector →a;→b không cùng phương và vector →c. Khi đó ba vector →a;→b;→c đồng phẳng khi và chỉ khi tồn tại cặp số m;n sao cho →c=m→a+n→b. Ngoài ra cặp số m;n là duy nhất.
Lời giải chi tiết
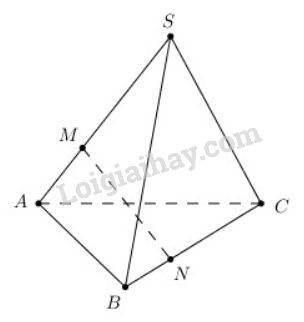
Biểu diễn →MN qua hai véc tơ →AB,→SC:
Ta có:
→MN=→MS+→SC+→CN=23→AS+→SC+23→CB(1)
→MN=→MA+→AB+→BN=−13→AS+→AB−13→CB(2)
Nhân (2) với 2 rồi cộng với (1) ta được:
3→MN = →SC + 2→AB ⇔→MN=13→SC+23→AB.
Vậy →AB, →MN, →SC đồng phẳng.

