Video hướng dẫn giải
LG a
Vẽ đồ thị của hàm số f(x)=x22
Lời giải chi tiết:
LG b
Tính f′(1).
Lời giải chi tiết:
- Giả sử Δx là số gia của đối số tại x0=1. Ta có:
Δy=f(1+Δx)−f(1)=(1+Δx)22−122=(Δx)2+2Δx2⇒ΔyΔx=(Δx)2+2Δx2:Δx=Δx2+1⇒f′(1)=limΔx→0ΔyΔx=limΔx→0Δx2+1=0+1=1
LG c
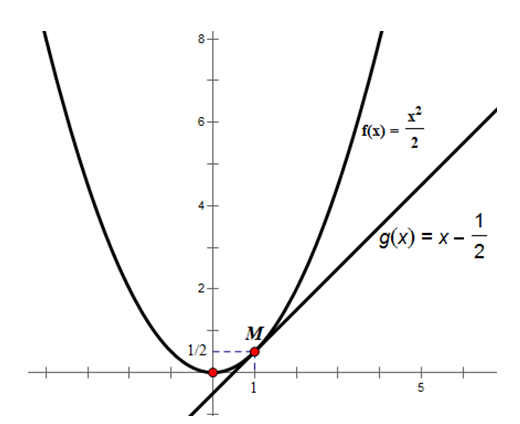
Vẽ đường thẳng đi qua điểm M(1;12) và có hệ số góc bằng f′(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.
Lời giải chi tiết:
- Đường thẳng có hệ số góc bằng f′(1)=1 có dạng:
y=1.x+a hay y=x+a
Mà đường thẳng đó đi qua điểm M(1;12) nên có: 12=1+a⇒a=12−1=−12
⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y=x–12
Ta có đồ thị như trên. Đường thẳng y=x–12 tiếp xúc với đồ thị hàm số f(x) tại M