Đề bài
Cho hình lập phương ABCD.A′B′C′D′ có E và F lần lượt là trung điểm của các cạnh AB và DD′. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC′) và (EFK) với K là trung điểm của cạnh B′C′.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định giao tuyến của các mặt phẳng đã cho với tất cả các mặt của hình lập phương.
Lời giải chi tiết
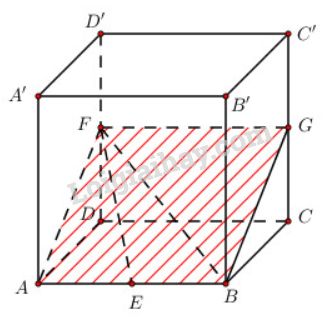
- Mặt phẳng (EFB) chính là mặt phẳng (ABF), mặt phẳng này chứa cạnh AB//CD nên (EFB)∩(DCC′D′)=GF//AB(G∈CC′)
Ta có thiết diện là hình bình hành ABGF như hình dưới đây.
Tuy nhiên ta lại có AB⊥(ADD′A′)⇒AB⊥AF⇒ABGF là hình chữ nhật.
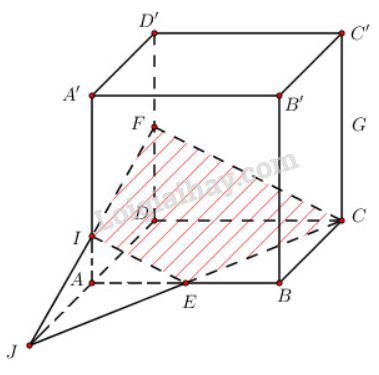
- Trong mặt phẳng (ABCD),CE∩DA tại J. Trong mặt phẳng (ADD′A′) có JF∩AA′ tại I.
Thiết diện cần dựng là hình thang CFIE (IE//FC) như hình dưới đây:
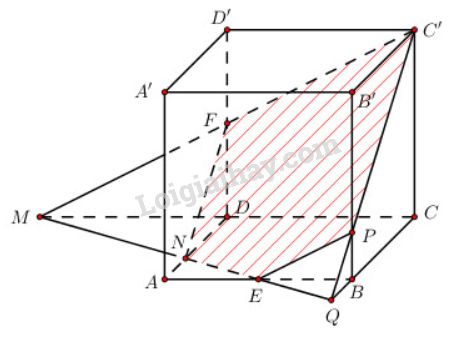
- Trong mặt phẳng (DCC′D′), C′F∩CD tại M. Trong mặt phẳng (ABCD), EM∩AD tại N, FN là giao tuyến của mặt phẳng (C′EF) với mặt bên (ADD′A′).
Trong mặt phẳng (ABCD), ME∩BC tại Q. Trong mặt phẳng (BCC′B′), C′Q∩BB′ tại P.
Thiết diện cần dựng là hình ngũ giác C′PENF như hình dưới đây:
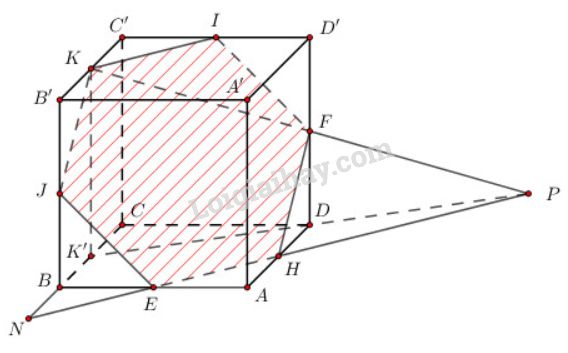
- Gọi E,H,F,I,K,J theo thứ tự là trung điểm của AB,AD,DD′,D′C′,C′B′,BB′. Ta dễ dàng chứng minh được 6 điểm E,H,F,I,K,J nằm trên cùng một mặt phẳng. Mặt phẳng này chính là mặt phẳng (EFK) và thiết diện có được là hình lục giác EHFIKJ. Lục giác này có ba cặp cạnh đối song song và bằng nhau nên nó là lục giác đều. Hình dưới đây: