Video hướng dẫn giải
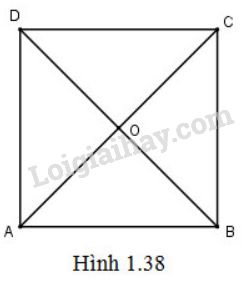
Cho hình vuông ABCDABCD tâm OO (h.1.38)
LG a
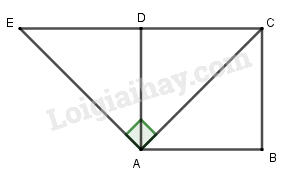
Tìm ảnh của điểm CC qua phép quay tâm AA góc 90∘90∘
Phương pháp giải:
Xác định ảnh:
+) Nối CC với AA, vẽ tia AtAt (về phía ngược chiều kim đồng hồ so với tia ACAC) sao cho ^CAt=900.ˆCAt=900.
+) Trên tia AtAt, lấy điểm EE sao cho AC=AE.AC=AE.
Chỉ ra vị trí của điểm E.E.
Cách khác: Lấy EE, chứng tỏ EE là ảnh của CC qua phép quay đó.
Lời giải chi tiết:
Gọi EE là điểm đối xứng với CC qua tâm DD. Ta có: tam giác ACE vuông cân tại A.
⇒{AC=AE(AC,AE)=900
Khi đó Q(A,90∘) (C) = E
LG b
Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90∘
Lời giải chi tiết:
{OC=OB(OB,OC)=900 ⇒Q(O,900)(B)=C
{OD=OC(OC,OD)=900 ⇒Q(O,900)(C)=D
Vậy ảnh của đường thẳng BC qua phép quay tâm O góc 90∘ là đường thẳng CD.