Đề bài
Cho hai đường thẳng \(a\) và \(b\) song song với nhau. Hãy chỉ ra một phép tịnh tiến biến \(a\) thành \(b\). Có bao nhiêu phép tịnh tiến như thế?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu.
+ Để tìm ảnh của môt đường thẳng qua phép tịnh tiên ta tìm ảnh của hai điểm thuộc đường thẳng đó qua phép tịnh tiến.
Lời giải chi tiết
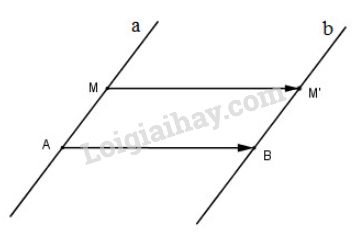
+ Lấy điểm \(A\) bất kì thuộc \(a\) và điểm \(B\) bất kì thuộc \(b\).
Ta sẽ chứng minh mọi phép tịnh tiến theo \(\overrightarrow{AB}\) biến \(a\) thành \(b\).
+ Trên \(a\) lấy \(M\) bất kì, gọi \(M'\) = \(T_{\vec{AB}}\) \((M)\). Ta chứng minh \(M' \in b\)
Vì: \(M'\) = \(T_{\vec{AB}}\) \((M)\) nên \(\overrightarrow{MM'}\)= \(\overrightarrow{AB}\).
Suy ra tứ giác \(AMM'B\) là hình bình hành, hay \(AM // BM' \)
Vậy \(M' \in b\) hay \(BM'\) trùng với \(b\)
+ Ta có: \(A, M \in a\) nên \(T_{\vec{AB}}\) \((a)\) là đường thẳng đi qua \(T_{\vec{AB}}\) \((A)\) và \(T_{\vec{AB}}\) \((M)\)
Mà: \(B = T_{\vec{AB}}\) \((A)\) và \(M' = T_{\vec{AB}}\) \((M)\)
\(\Rightarrow b = T_{\vec{AB}}\) \((a)\)
Vì \(A,B\) là các điểm bất kì ( trên \(a\) và \(b\) tương ứng) nên có vô số phép tịnh tiến biến \(a\) thành \(b\).

