Đề bài
Cho tam giác ABCABC có ba góc nhọn và HH là trực tâm. Tìm ảnh của tam giác ABCABC qua phép vị tự tâm HH, tỉ số 12.12.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tìm ảnh của từng đỉnh. Ảnh của tam giác là tam giác tạo bởi ba điểm ảnh đó.
+) V(H,12)(M)=M′⇔→HM′=12.→HM
Lời giải chi tiết
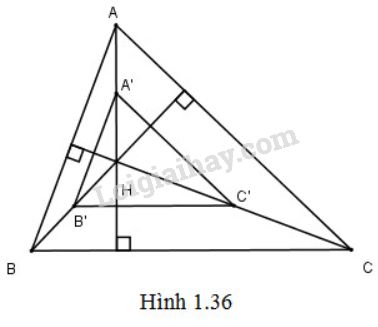
Gọi A′,B′,C′ lần lượt là ảnh của A,B,C qua V(H,12) ta có:
+) A′=V(H,12)(A)⇒→HA′=12→HA⇒A′ là trung điểm của AH.
+) B′=V(H,12)(B)⇒→HB′=12→HB⇒B′ là trung điểm của BH.
+) C′=V(H,12)(C)⇒→HC′=12→HC⇒C′ là trung điểm của CH.
Vậy V(H,12)(ΔABC)=A′B′C′, trong đó A′,B′,C′ lần lượt là trung điểm của HA,HB,HC.

