Cho hàm số
f(x)=x2−2xx−1
LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số f
Lời giải chi tiết:
TXĐ: D=R∖{1}
y=x2−2xx−1=x−1−1x−1y′=1+1(x−1)2>0
⇒Hàm số đồng biến trên (−∞;1) và (1;+∞).
lim
\mathop {\lim }\limits_{x \to + \infty } \left( {y - x + 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{ - 1}}{{x - 1}} = 0
\Rightarrow x = 1;y = x - 1 lần lượt là tiệm cận đứng và tiệm cận xiên của đồ thị
Bảng biến thiên:
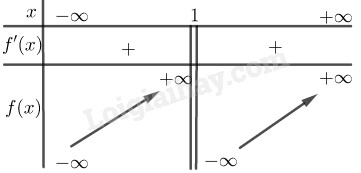
Đồ thị:
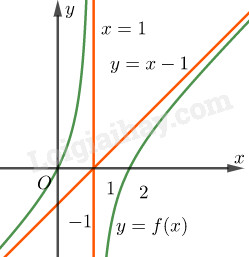
LG b
Từ đồ thị (C) suy ra cách vẽ đồ thị hàm số
g\left( x \right) = {{{x^2} - 2\left| x \right|} \over {\left| x \right| - 1}}
Lời giải chi tiết:
g là một hàm số chẵn nên đồ thị ({C_1}) của đồ thị đối xứng qua trục tung. Với x \ge 0, ta có
g\left( x \right) = {{{x^2} - 2x} \over {x - 1}} = f\left( x \right)
Do đó, muốn có đồ thị \left( {{C_1}} \right) của hàm số g ta bỏ đi phần đường cong (C) nằm bên trái trục tung, giữ lại phần của đường cong (C) nằm bên phải trục tung (ứng với các giá trị x \ge 0,x \ne 1) và bổ xung thêm hình đối xứng của phần đường cong này qua trục tung.
LG c
Với các giá trị nào của m thì phương trình
{x^2} - 2\left| x \right| = m\left( {\left| x \right| - 1} \right)
có bốn nghiệm thực phân biệt ?
Lời giải chi tiết:
m > 0
Phương trình đã cho tương đương với phương trình
{{{x^2} - 2\left| x \right|} \over {\left| x \right| - 1}} = m
Số nghiệm của phương trình đã cho bằng số giao điểm \left( {{C_1}} \right) và đường thẳng y = m

