Cho hình nón N có bán kính đáy R, góc giữa đường sinh và đáy của hình nón bằng \(\alpha \). Một mặt phẳng (P) song song với đáy hình nón, cách đáy hình nón một khoảng h và cắt hình nón theo đường tròn (C ).
LG 1
Tính bán kính đường tròn (C ) theo R, h,a.
Lời giải chi tiết:
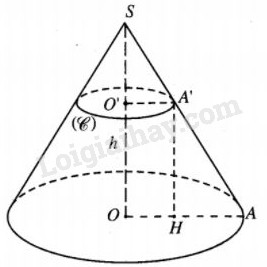
Gọi đường cao của hình nón là SO, một đường sinh của hình nón là SA thì \(\widehat {SAO} =\alpha \)
Gọi O’, A’ lần lượt là giao của SO, SA với mp(P) và H là hình chiếu của A’ trên OA thì
\(AH = A'H.\cot \alpha = h.cot\alpha \)
Và bán kính của đường tròn (C ) là
\(R' = O'A' = OA - HA = R - h.\cot \alpha .\)
LG 2
Tính diện tích và thể tích phần hình nón nằm giữa đáy hình nón N và mặt phẳng (P).
Lời giải chi tiết:
\( \bullet \) Gọi \({S_1}\) là phần diện tích phải tìm, \({S_2}\) là phần diện tích xung quanh hình nón đỉnh S và đáy là (C ). Khi đó \({S_1} = S - {S_2}\) ( S là diện tích xung quanh của hình nón N ), tức là
\(\eqalign{ {S_1} &= \pi R.SA - \pi R'.SA' \cr & = \pi \left( {R.{R \over {\cos \alpha }} - R'.{{R'} \over {\cos \alpha }}} \right) \cr & = {\pi \over {\cos \alpha }}\left[ {{R^2} - {{(R - h.\cot \alpha )}^2}} \right] \cr & = {\pi \over {\cos \alpha }}h.\cot \alpha (2R - h.\cot \alpha ) \cr&= {{\pi h} \over {\sin \alpha }}(2R - h.\cot \alpha ). \cr} \)
\( \bullet \) Gọi V1 là phần thể tích cần tìm, V2 là phần thể tích khối nón đỉnh S và đáy là đường tròn (C ). Khi đó
\({V_1} = V - {V_2}\) (V là thể tích hình nón đã cho)
\(\eqalign{ & = {1 \over 3}\pi {R^2}.SO - {1 \over 3}\pi R{'^2}.SO' \cr & = {1 \over 3}\pi ({R^2}.R\tan \alpha - R{'^2}.R'\tan \alpha ) \cr & = {1 \over 3}\pi \tan \alpha ({R^3} - R{'^2}) \cr & = {1 \over 3}\pi \tan \alpha \left[ {{R^3} - {{(R - h\cot \alpha )}^3}} \right] \cr & = {{\pi h} \over 3}(3{R^2} - 3Rh\cot \alpha + {h^2}{\cot ^2}\alpha ). \cr} \)

