Đề bài
Khối chóp S.ABCD có SA⊥(ABC); đáy là tam giác ABC cân tại A, độ dài trung tuyến AD bằng a, cạnh bên SB tạo với đáy một góc α và tạo với mặt (SAD) góc β. Tính thể tích khối chóp.
Lời giải chi tiết
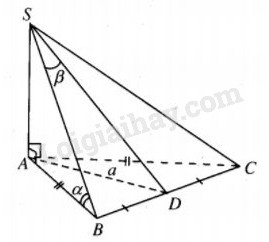
AB là hình chiếu của SB trên mp(ABC) nên ^SBA=α
Dễ thấy BD⊥(SAD) nên hình chiếu của SB trên mp(SAD) là SD ⇒ ^BSD=β
Do SAB và SDB là các tam giác vuông nên ta có SB=BDsinβ,SB=ABcosα, suy ra
AB2cos2α=BD2sin2β=AB2−BD2cos2α−sin2β=a2cos2α−sin2β⇒BD=asinβ√cos2α−sin2β,
SD=BDcotβ=acosβ√cos2α−sin2β,SA=√SD2−AD2=asinα√cos2α−sin2β.
Vậy :
VS.ABC=13SABC.SA=13.a.asinβ√cos2α−sin2β.asinα√cos2α−sin2β=a3sinα.sinβ3(cos2α−sin2β).

