Cho hình chóp S.ABCD, đáy ABCD là tứ giác có hai đường chéo vuông góc với nhau tại H và SH là đường cao của hình chóp đã cho.
LG 1
Chứng minh rằng bốn tâm mặt cầu ngoại tiếp các hình chóp S.HAB, S.HBC, S.HCD, S.HDA là bốn đỉnh của một hình chữ nhật.
Lời giải chi tiết:
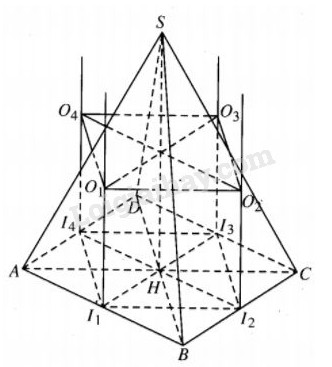
Gọi I1 là trung điểm của AB và O1 là tâm mặt cầu ngoại tiếp hình chóp S.ABH thì I1O1//SHI1O1//SH và I1O1=12SH.I1O1=12SH.
Tương tự như trên, nếu I2,I3,I4I2,I3,I4 thứ tự là trung điểm của BC, CD, DA và O2,O3,O4O2,O3,O4 thứ tự là tâm của mặt cầu ngoại tiếp các hình chóp S.HBC, S.HCD, S.HDA thì
I2O2=12SH,I3O3=12SH,I4O4=12SH,
và I2O2,I3O3,I4O4 cùng song song với SH.
Dễ thấy I1I2//O1O2 và I1I2//AC,
I2I3//O2O3 và I2I3//BD,
I3I4//O3O4 và I3I4//AC,
I4I1//O4O1 và I4I1//BD.
Kết hợp với AC⊥BD, ta có O1O2O3O4 là hình chữ nhật.
LG 2
Gọi H1, H2, H3, H4 là hình chiếu của H lần lượt trên AB, BC, CD, DA . Chứng minh rằng hình chóp S. H1H2H3H4 có mặt cầu ngoại tiếp. Tính diện tích của thiết diện của mặt cầu ấy khi cắt bởi mp(ABCD) nếu biết H1H3 =a,^BAC=α,^BDC=β
Lời giải chi tiết:
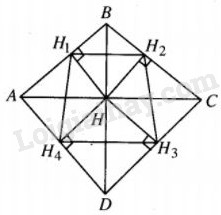
Dễ thấy ^HH1H2=^HBH2=^HBC,
^HH1H4=^HAH4=^HAD,
^HH3H2=^HCH2=^HCB,
^HH3H4=^HDH4=^HDA
Từ đó
^HH1H2+^HH1H4+^HH3H2+^HH3H4
=^HBC+^HCB+^HAD+^HDA=1800
Vậy H1H2H3H4 là tứ giác nội tiếp đường tròn.
Từ đó hình chóp S. H1H2H3H4 có mặt cầu ngoại tiếp.
Diện tích thiết diện của hình cầu đó và mặt phẳng (ABCD) là diện tích hình tròn ngoại tiếp tứ giác H1H2H3H4.
Vì ^BAC=α,^BDC=β nên ^H1H4H3=α+β. Khi ấy H1H3sin(α+β)=2R (R là bán kính đường tròn ngoại tiếp tứ giác H1H2H3H4), từ đó R=a2sin(α+β).
Vậy diện tích hình thu được là
4πR2=πa2sin2(α+β).

